
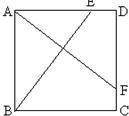
 24、如图,是一个正方形花园ACBD,E,F是它的两个门,且DE=CF,要修建两条路BE,AF,问这两条路长相等吗?它们有什么位置关系.
24、如图,是一个正方形花园ACBD,E,F是它的两个门,且DE=CF,要修建两条路BE,AF,问这两条路长相等吗?它们有什么位置关系. 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
 30、如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各脚处的正方形观光休息亭的边长为多少米?
30、如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各脚处的正方形观光休息亭的边长为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?
如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?查看答案和解析>>
科目:初中数学 来源:2011年中考数学复习第二单元《方程(组)与不等式(组)》测试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《一元二次方程》(04)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年湖北省襄樊市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com