
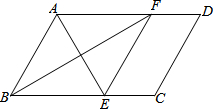
 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.分析 (1)根据平行四边形的性质和角平分线的性质证明∠BAE=∠BEA,从而可得AB=BE,同理可得AB=AF,再由AF∥BE可得四边形ABEF是菱形;
(2)过A作AH⊥BE,根据菱形的性质可得AO=EO,BO=FO,BE=AB=5,AE⊥BF,利用勾股定理可得AO的长,进而可得AE长,利用菱形的面积公式计算出AH的长,然后可得?ABCD的面积.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,
同理:AB=AF,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF
∴四边形ABEF是菱形.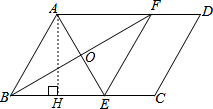
(2)解:过A作AH⊥BE,
∵四边形ABCD是菱形,
∴AO=EO,BO=FO,BE=AB=5,AE⊥BF,
∵BF=8,
∴BO=4,
∴AO=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AE=6,
∴S菱形ABEF=$\frac{1}{2}$AE•BF=$\frac{1}{2}$×6×8=24,
∴BE•AH=24,
∴AH=$\frac{24}{5}$,
∵四边形ABCD是平行四边形,
∴BC=AD=$\frac{15}{2}$,
∴S平行四边形ABCD=$\frac{15}{2}$×$\frac{24}{5}$=36,
故答案为:36.
点评 此题主要考查了菱形的性质和判定,以及平行四边形的性质,关键是掌握邻边相等的平行四边形是菱形,菱形的面积为对角线之积的一半.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
 阅读理解:
阅读理解:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰三角形ABC中,AC=BC=10,AB=12.
如图,等腰三角形ABC中,AC=BC=10,AB=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,以A(1,1)为顶点的抛物线y=x2-2x+c与y轴交于点C,正方形ABCD的边CD与y轴重合,点P为第一象限内抛物线上的点且不与点A重合,过点P作PF∥x轴交y轴于点F,PE∥y轴交x轴于点E.设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为L.
如图,在平面直角坐标系中,以A(1,1)为顶点的抛物线y=x2-2x+c与y轴交于点C,正方形ABCD的边CD与y轴重合,点P为第一象限内抛物线上的点且不与点A重合,过点P作PF∥x轴交y轴于点F,PE∥y轴交x轴于点E.设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为L.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{x+3≥6}\\{2x-1≤9}\end{array}\right.$,并写出它的所有整数解.
解不等式组$\left\{\begin{array}{l}{x+3≥6}\\{2x-1≤9}\end{array}\right.$,并写出它的所有整数解.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 3 | C. | 6 | D. | 3$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com