Question

4．已知：△ABC中，AB=AC，∠B=α．
（1）如图1，点D，E分别在边AB，AC上，线段DE的垂直平分线MN交直线BC于点M，交DE于点N，求证：BD+CE=BC．需补充条件∠EMN=$\frac{1}{2}$α（用含α的式子表示）补充条件后并证明；
（2）把（1）中的条件改为点D，E分别在边BA、AC延长线上，线段DE的垂直平分线MN交直线BC于点M，交DE于点N（如图2），并补充条件∠EMN=$\frac{1}{2}$α（用含α的式子表示），通过观察或测量，猜想线段BD，CE与BC之间满足的数量关系，并予以证明．

Answer 1

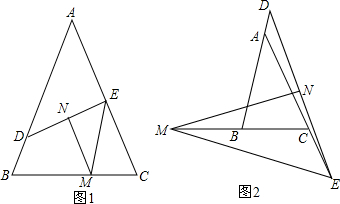
分析 （1）当∠EMN=$\frac{1}{2}$α时，BD+CE=BC．连接DM．先证明∠DME=α．接下来证明∠DMB=∠CEM．然后依据AAS可证明△BDM≌△CME，然后由全等三角形的性质可证得BD=MC，EC=BM，结合条件MB+MC=BC，可证得问题的结论；
（2）当∠EMN=$\frac{1}{2}$α时，BD=CE+BC．先证明∠DMN=∠EMN=$\frac{1}{2}$α．从而得到∠EMD=∠B=α，接下来，依据等角的补角相等可证得∠DBM=∠MCE，然后依据三角形的外角的性质和角的和差关系证明∠MDB=∠EMC，然后依据AAS可证明△BDM≌△CME，由全等三角形的性质可得到BD=MC，EC=BM，结合MB+BC=MC可证得EC+BC=BD．

解答 解：（1）当∠EMN=$\frac{1}{2}$α时，BD+CE=BC．
理由：如图1所示：连接DM．

∵AB=AC，
∴∠B=∠C=α．
∵MN是DE的垂直平分线，
∴DN=NE，DM=EM．
在△MND和△MNE中，
$\left\{\begin{array}{l}{ND=NE}\\{MN=MN}\\{DM=ME}\end{array}\right.$，
∴△MND≌△MNE．
∴∠DMN=∠EMN=$\frac{1}{2}$α．
∴∠DME=α．
∵∠C+∠CEM=∠DMB+∠DME，∠C=∠DME=α，
∴∠DMB=∠CEM．
在△BDM和△CME中，
$\left\{\begin{array}{l}{∠B=∠C}\\{∠DMB=∠CEM}\\{DM=EM}\end{array}\right.$，
∴△BDM≌△CME．
∴BD=MC，EC=BM．
又∵MB+MC=BC，
∴BD+EC=BC．
（2）当∠EMN=$\frac{1}{2}$α时，BD=CE+BC．

∵AB=AC，
∴∠ABC=∠ACB．
∴∠DBM=∠MCE．
∵MN是DE的垂直平分线，
∴DN=NE，DM=EM．
在△MND和△MNE中，
$\left\{\begin{array}{l}{ND=NE}\\{MN=MN}\\{DM=ME}\end{array}\right.$，
∴△MND≌△MNE．
∴∠DMN=∠EMN=$\frac{1}{2}$α．
∴∠EMD=∠B=α
∵∠BMD+∠MDB=α，∠EMC+∠CMD=α，
∴∠EMC=∠MDB．
在△BDM和△CME中，
$\left\{\begin{array}{l}{∠DBM=∠MCE}\\{∠MDB=∠EMC}\\{MD=ME}\end{array}\right.$，
∴△BDM≌△CME．
∴BD=MC，EC=BM．
又∵MB+BC=MC，
∴EC+BC=BD．

点评 本题主要考查的是三角形的综合应用，解答本题主要应用了等腰三角形的性质、全等三角形的性质和判定、线段垂直平分线的性质、三角形的外角的性质，熟练掌握相关性质是解题的关键．