
分析 (1)利用三角函数的定义求解;
(2)在Rt△BDE中,利用三角函数定义得到sin∠BDE=$\frac{BE}{BD}$=$\frac{4}{5}$,则可设BE=4x,BD=5x,于是根据勾股定理得到DE=3x,BC=2BD=10x,再利用余弦定义得到cosB=$\frac{BE}{BD}$=$\frac{BC}{AB}$,即$\frac{10x}{4x+3.4}$=$\frac{4}{5}$,然后利用比例性质求出x后即可得到DE的长.
解答 解:(1)在Rt△BDE中,sinB=$\frac{DE}{BD}$,tanB=$\frac{DE}{BE}$,cosB=$\frac{BE}{BD}$,
在Rt△ACB中,sinB=$\frac{AC}{AB}$,
sinA=$\frac{BC}{AB}$,tanB=$\frac{AC}{BC}$,
而∠A+∠B=90°,
所有sinA=cosB=$\frac{BE}{BD}$;
故答案为$\frac{DE}{BD}$,$\frac{AC}{AB}$;$\frac{BC}{AB}$或$\frac{BE}{BD}$;$\frac{AC}{BC}$或$\frac{DE}{BE}$;
(2)∵sin∠BDE=$\frac{BE}{BD}$=$\frac{4}{5}$,
∴设BE=4x,BD=5x,
∴DE=$\sqrt{(5x)^{2}-(4x)^{2}}$=3x,
∵D是BC的中点,
∴BC=2BD=10x,
∵cosB=$\frac{BE}{BD}$=$\frac{BC}{AB}$,
∴$\frac{10x}{4x+3.4}$=$\frac{4}{5}$,解得x=0.4,
∴DE=3x=1.2.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.


科目:初中数学 来源: 题型:解答题
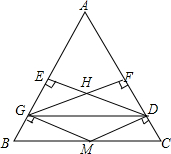 已知:如图,在△ABC中,AB=AC,点M在BC上,BM=CM,作MD⊥AC于D,MG⊥AB于G,GF⊥AC于F,DE⊥AB于E,GF、DE交于点H.求证:四边形MDHG为菱形.
已知:如图,在△ABC中,AB=AC,点M在BC上,BM=CM,作MD⊥AC于D,MG⊥AB于G,GF⊥AC于F,DE⊥AB于E,GF、DE交于点H.求证:四边形MDHG为菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 总条数 | 50 | 45 | 60 | 48 | 10 | 30 | 42 | 38 | 15 | 10 |
| 标记数 | 2 | 1 | 3 | 2 | 0 | 1 | 1 | 2 | 0 | 1 |
| 总条数 | 53 | 36 | 27 | 34 | 43 | 26 | 18 | 22 | 25 | 47 |
| 标记数 | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com