
 如图,⊙O为△ABC的外接圆,弦CD平分△ABC的外角∠ACE.求证:OD⊥AB.
如图,⊙O为△ABC的外接圆,弦CD平分△ABC的外角∠ACE.求证:OD⊥AB. 分析 连结DA,CD平分△ABC的外角∠ACE,得到∠DCE=∠ACD,由圆内接四边形的性质得出∠DCE=∠BAD,进一步得出∠ACD=∠BAD,根据圆周角定理得$\widehat{BD}$=$\widehat{AD}$,根据垂径定理即可证得OD⊥AB.
解答 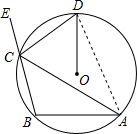 证明:连结DA,如图,
证明:连结DA,如图,
∵弦CD平分△ABC的外角∠ACE,
∴∠DCE=∠ACD,
∵四边形ABCD是圆内接四边形,
∴∠DCE=∠BAD,
∴∠ACD=∠BAD,
∴$\widehat{BD}$=$\widehat{AD}$,
∴OD⊥AB.
点评 本题考查了圆内接四边形的性质,垂径定理以及圆周角定理,熟练掌握性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
| 月 份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 销量(台) | 50 | 51 | 48 | 50 | 52 | 49 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=2,MC=6,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=2,MC=6,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )| A. | 2$\sqrt{10}$ | B. | 8 | C. | 2$\sqrt{17}$ | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在讲完《平行线的性质》后,老师出了一道题:如图所示,∠1=65°,∠2=∠65°,∠3=60°,求∠4的度数.小刚看了题目后说:“题中给出∠1和∠2的度数是多余的,因为∠3和∠5是一对同位角,而同位角相等,所以∠5=∠3=60°.又根据对顶角相等得∠4=∠5=60°.你认为小刚的说法对吗?并说明原因.
在讲完《平行线的性质》后,老师出了一道题:如图所示,∠1=65°,∠2=∠65°,∠3=60°,求∠4的度数.小刚看了题目后说:“题中给出∠1和∠2的度数是多余的,因为∠3和∠5是一对同位角,而同位角相等,所以∠5=∠3=60°.又根据对顶角相等得∠4=∠5=60°.你认为小刚的说法对吗?并说明原因.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com