练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠ACB =90°，AC = BC =2，AB =，点P是AB边上的点（异于点A，B），点Q是BC边上的点（异于点B，C），且∠CPQ =45°.当△CPQ是等腰三角形时，CQ的长为________.

    【答案】或1．

    【解析】

    分两种情形：①当PC=PQ时．②当PQ=CQ时分别求解即可.

    解：①当PC=PQ时，∵CA=CB=2，∠ACB=90°，

    ∴∠A=∠B=45°，AB=，

    ∵∠CPB=∠CPQ+∠QPB=∠A+∠ACP，∠CPQ=45°，

    ∴∠CPQ=∠A，

    ∴∠ACP=∠BPQ，

    ∴△ACP≌△BPQ，

    ∴AC=PB=2，AP=BQ=，

    ∴CQ=2-（）=，

    ②当PQ=CQ时，∠QPC=∠QCP=45°，

    ∴∠ACP=∠BCP=45°，∠PQC=90°，

    ∴PA=PB=PC，

    ∵PQ⊥BC，

    ∴CQ=BQ=1，

    故答案为：或1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读材料，并解决问题：

    我国古代数学的许多发现都曾居世界前列，“杨辉三角”就是其中一例．如图是“杨辉三角”的一部分，其构造法则为：两腰上的数都是1，其余每个数均为其上方左右两数之和，“杨辉三角”给出了（为正整数）的展开式（按的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应展开式中的系数；第四行的四个数1，3，3，1，恰好对应着展开式中的系数．

    （1）根据上面的规律，直接写出的展开式共有_______项；

    （2）直接写出的展开式；

    （3）利用上面的规律计算：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】知图①，在数轴上有一条线段，点表示的数分别是和．

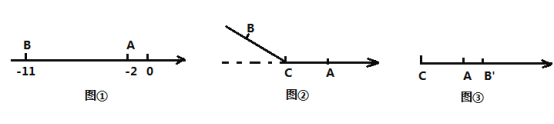
    （1）线段____________；

    （2）若是线段的中点，则点在数轴上对应的数为________；

    （3）若为线段上一点．如图②，以点为折点，将此数轴向右对折；如图③，点落在点的右边点处，若，求点在数轴上对应的数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图 ，BE平分△ABC的外角∠ABD，F是 AC的中点，过 F点作 AC的垂线交 BE的反向延长线于 G点， 连 EG．若∠ABC＝80°，则∠ACG的度数为是_____

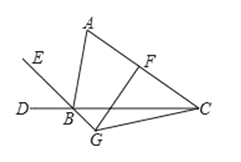
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究活动：

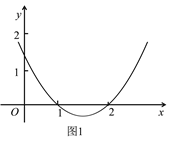
    利用函数的图象(如图1)和性质，探究函数的图象与性质．

    下面是小东的探究过程，请补充完整：

    （1）函数的自变量x的取值范围是___________；

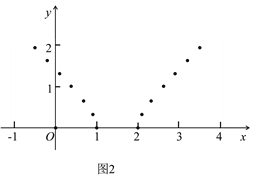
    （2）如图2，小东列表描出了函数图象上部分点，请画出函数图象；

    （3）解决问题：设方程的两根为、，且，方程

    的两根为、，且．若，则、、、的大小关系为_____________________（用“<”连接）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

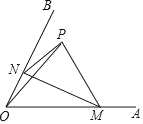
    【题目】如图，∠AOB=60°，点P是∠AOB内的定点且OP=，若点M、N分别是射线OA、OB上异于点O的动点，则△PMN周长的最小值是（　　）

    A. B. C. 6 D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

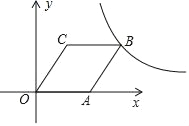
    【题目】如图，在平面直角坐标系中，点O为坐标原点，菱形OABC的顶点A在x轴的正半轴上，顶点C的坐标为（1，）．

    （1）求图象过点B的反比例函数的解析式；

    （2）求图象过点A，B的一次函数的解析式；

    （3）在第一象限内，当以上所求一次函数的图象在所求反比例函数的图象下方时，请直接写出自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把边长为1厘米的6个相同正方体摆成如图的形式．

    （1）该几何体的表面积为___________；

    （2）如果在这个几何体上再添加一些相同的小正方体，使得从上面和从左面看到的图形保持不变，那么最多可以再添加__________个小正方体，并在下面的方格纸中画出添加小正方体后你从正面所看到的几何体形状图（画出符合条件中的一种即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的任意两点M(x1，y1)，N(x2，y2)，给出如下定义：

    将|x1﹣x2|称为点M，N之间的“横长”，|y1﹣y2|称为点M，N之间的纵长”，点M与点N的“横长”与“纵长”之和称为“折线距离”，记作d(M，N)=|x1﹣x2|+|y1﹣y2|“．

    例如：若点M(﹣1，1)，点N(2，﹣2)，则点M与点N的“折线距离”为：d(M，N)=|﹣1﹣2|+|1﹣(﹣2)|=3+3=6．

    根据以上定义，解决下列问题：

    已知点P(3，2)．

    （1）若点A(a，2)，且d(P，A)=5，求a的值；

    （2）已知点B(b，b)，且d(P，B)＜3，直接写出b的取值范围；

    （3）若第一象限内的点T与点P的“横长”与“纵长”相等，且d(P，T)＞5，简要分析点T的横坐标t的取值范围．

    查看答案和解析>>

    同步练习册答案