
【题目】如图,在![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
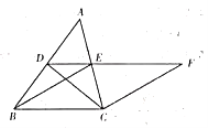
(1)求证:四边形![]() 是菱形;
是菱形;
(2)在不添加任何辅助线和字母的情况下,请直接写出图中与![]() 面积相等的所有三角形(不包括
面积相等的所有三角形(不包括![]() ).
).
【答案】(1)证明见解析;(2)![]() 、
、![]() 、
、![]() 、
、![]() .
.
【解析】
(1)由题意易得,EF与BC平行,结合![]() ,可得四边形BCFE是平行四边形,然后求出邻边
,可得四边形BCFE是平行四边形,然后求出邻边![]() ,则四边形BCFE是菱形;
,则四边形BCFE是菱形;
(2)根据等底等高的两个三角形面积相等以及三角形的中线将三角形分成面积相等的两部分进行求解即可.
(1)证明:∵![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴平行四边形![]() 是菱形;
是菱形;
(2)解:①∵由(1)知,四边形BCFE是菱形,
∴BC=FE,BC∥EF,
∴△FEC与△BEC是等底等高的两个三角形,
∴S△FEC=S△BEC;
②△AEB与△BEC是等底同高的两个三角形,则S△AEB=S△BEC;
③S△ADC=![]() S△ABC,S△BEC=
S△ABC,S△BEC=![]() S△ABC,则S△ADC=S△BEC;
S△ABC,则S△ADC=S△BEC;
④S△BDC=![]() S△ABC,S△BEC=
S△ABC,S△BEC=![]() S△ABC,则S△BDC=S△BEC.
S△ABC,则S△BDC=S△BEC.
综上所述,与△BEC面积相等的三角形有:△FEC、△AEB、△ADC、△BDC.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在下列4×4(边长为1)的网格中,已知△ABC的三个顶点A,B,C在格点上,请分别按不同要求在网格中描出一个格点D,并写出点D的坐标.
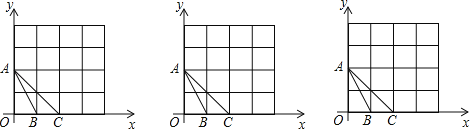
(1)将△ABC绕点C顺时针旋转90°,画出旋转后所得的三角形,点A旋转后落点为D;
(2)经过A,B,C三点有一条抛物线,请找到点D,使点D也落在这条抛物线上;
(3)经过A,B,C三点有一个圆,请找到一个横坐标为2的点D,使点D也落在这个圆上,
①点D的坐标为 ;
②点D的坐标为 ;
③点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
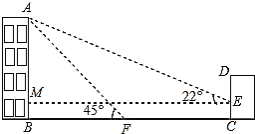
【题目】如图,某办公楼AB的右边有一建筑物CD,在建设物CD离地面2米高的点E处观测办公楼顶A点,测得的仰角![]() =
=![]() ,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角
,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角![]() =
=![]() (B,F,C在一条直线上).
(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生200米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
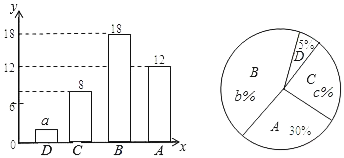
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生200米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
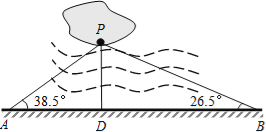
【题目】如图,益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠PAB=38.5°,∠PBA=26.5.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)
(参考数据:sin38.5°=0.62,cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示:下列4个结论
①abc<0
②b>2ac
③ax2+bx+c=0的两根分别为﹣3和1
④a﹣2b+c>0
其中正确的是( )
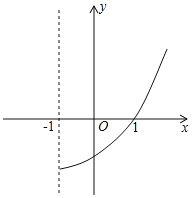
A.①②B.②③C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB>AD,∠A=60°,
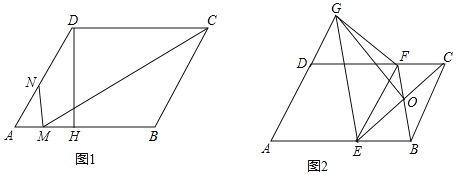
(1)如图1,过点D作DH⊥AB于点H,MC平分∠DCB交AB边于点M,过M作MN⊥AB交AD边于点N,AN:ND=2:3,平行四边形ABCD的面积为60![]() ,求MN的长度.
,求MN的长度.
(2)如图2,E、F分别为边AB、CD上一点,且AE=AD=DF,连接BF、EC交于点O,G为AD延长线上一点,连接GE、GF和GO,若∠GFD=∠EFB,求证:GO⊥EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
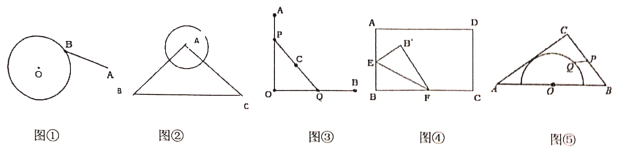
【题目】阅读下列材料,回答问题.
材料:求圆外一定点到圆上距离最小值是安徽省中考数学较为常见的一种题型,此类题型试题有时出题者将圆隐藏,故又称为“隐圆问题”.解决这类问题,关键是要找到动点的运动轨迹,即该动点是绕哪一个定点旋转,且能保持旋转半径不变.从而找到动点所在的隐藏圆,进面转换成圆外一点到圆心的距离减半径,求得最小值.
解决问题:
(1)如图①,圆O的半径为1,圆外一点A到圆心的距离为3,圆上一动点B,当A、O、B满足条件____________时,![]() 有最小值为____________.
有最小值为____________.
(2)如图②,等腰![]() 两腰长为5,底边长为6,以A为圆心,2为半径作圆,圆上动点P到
两腰长为5,底边长为6,以A为圆心,2为半径作圆,圆上动点P到![]() 的距离最小值为__________.
的距离最小值为__________.
(3)如图③,![]() ,P、Q分别是射线
,P、Q分别是射线![]() 、
、![]() 上两个动点,C是线段
上两个动点,C是线段![]() 的中点,且
的中点,且![]() ,则在线段
,则在线段![]() 滑动的过程中,求点C运动形成的路径长,并说明理由.
滑动的过程中,求点C运动形成的路径长,并说明理由.
(4)如图④,在矩形![]() 中,
中,![]() ,
,![]() ,点E是
,点E是![]() 中点,点F是
中点,点F是![]() 上一点,把
上一点,把![]() 沿着
沿着![]() 翻折,点B落在点
翻折,点B落在点![]() 处,求
处,求![]() 的最小值,并说明理由.
的最小值,并说明理由.
(5)如图⑤,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以边
,以边![]() 中点O为圆心,作半圆与
中点O为圆心,作半圆与![]() 相切,点P,Q分别是边
相切,点P,Q分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,求
,求![]() 长的最小值,并说明理由.
长的最小值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com