
【题目】如图,在平面直角坐标系中线段AB的两个端点分别在坐标轴上,点A的坐标为(1,0),将线段AB绕点A顺时针旋转90°后,点B恰好落在反比例函数y=![]() 在第一象限内的分支上的点B′,则点B的坐标为( )
在第一象限内的分支上的点B′,则点B的坐标为( )
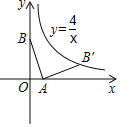
A.(0,2)B.(0,3)C.(0,4)D.(0,5)
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
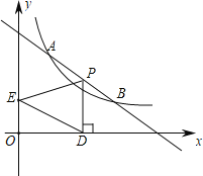
【题目】如图,直线y1=k1x+b与双曲线![]() 在第一象限内交于A、B两点,已知A(1,m),B(2,1).
在第一象限内交于A、B两点,已知A(1,m),B(2,1).
(1)直接写出不等式y2>y1的解集;
(2)求直线AB的解析式;
(3)设点P是线段AB上的一个动点,过点P作PD⊥x轴于点D,E是y轴上一点,求△PED的面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一前夕某幼儿园园长到厂家选购A、B两种品牌的儿童服装每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍,求A、B两种品牌服装每套进价分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AD=3,DC=4,动点P在线段DC上以每秒1个单位的速度从点D向点C运动,过点P作PQ∥AC交AD于Q,将△PDQ沿PQ翻折得到△PQE. 设点P的运动时间为t(s).
(1)当点E落在边AB上时,t的值为 ;
(2)设△PQE与△ADC重叠部分的面积为s,求s与t的函数关系式;
(3)如图2,以PE为直径作⊙O.当⊙O与AC边相切时,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
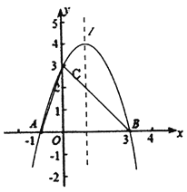
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:所有正整数在进行某种规定步骤的运算后,会得到一个恒定不变的数,我们把这个恒定不变的数叫做稳定数.规定求三位数的稳定数的运算步骤是:任意三位数A=![]() (百位与个位不相同),将这个数逆置后得A1=
(百位与个位不相同),将这个数逆置后得A1=![]() ,A与A1中较大的数减去较小的数得到一个数B,再将B进行一次逆置得B1(若B为两位数则交换十位与个位逆置),将B1与B相加得C,C就是该三位数A的稳定数,记作
,A与A1中较大的数减去较小的数得到一个数B,再将B进行一次逆置得B1(若B为两位数则交换十位与个位逆置),将B1与B相加得C,C就是该三位数A的稳定数,记作![]() .
.
材料二:当两个三位数的稳定数相同时,这两个三位数的百位数字与个位数字之差的绝对值或者都大于1,或者都等于1.
(1)求352的稳定数是 ;百位与个位相差2的三位数,它的稳定数是 .
(2)现有S=301+10p,T=100m+40+n(1≤p≤9,1≤m≤9,1≤n≤9,p,m,n均是整数),其中T是偶数,若![]() ,3p+m+n=20,|p-n|=1,
,3p+m+n=20,|p-n|=1,![]() ,请求出
,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过
经过![]() 点,直线
点,直线![]() 是抛物线的对称轴.
是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 的周长最小,求出点
的周长最小,求出点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上一动点,当
是抛物线上一动点,当![]() 时,请直接写出点
时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中有2枚黑棋,x枚白棋,这些棋子除颜色外无其他差别,现从盒中随机摸出一枚棋子(不放回),再随机摸出一枚棋子.
(1)若“摸出两枚棋子的颜色都是白色”是不可能事件,请写出符合条件的一个x值 ;
(2)当x=2时,“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com