
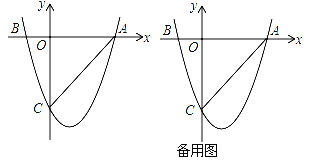
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø3£¬0£©£¬B£Ø©1£¬0£©Į½µć£¬ÓėyÖįĻą½»ÓŚµćC£Ø0£¬©3£©
£Ø1£©Ēóøƶž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ÉčEŹĒyÖįÓŅ²ąÅ×ĪļĻßÉĻŅģÓŚµćAµÄŅ»øö¶Æµć£¬¹żµćE×÷xÖįµÄĘ½ŠŠĻß½»Å×ĪļĻßÓŚĮķŅ»µćF£¬¹żµćF×÷FG“¹Ö±ÓŚxÖįÓŚµćG£¬ŌŁ¹żµćE×÷EH“¹Ö±ÓŚxÖįÓŚµćH£¬µĆµ½¾ŲŠĪEFGH£¬ŌņŌŚµćEµÄŌĖ¶Æ¹ż³ĢÖŠ£¬µ±¾ŲŠĪEFGHĪŖÕż·½ŠĪŹ±£¬Ēó³öøĆÕż·½ŠĪµÄ±ß³¤£»
£Ø3£©ÉčPµćŹĒxÖįĻĀ·½µÄÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓPA”¢PC£¬Ēó”÷PACĆ껿µÄȔֵ·¶Ī§£¬Čō”÷PACĆ껿ĪŖÕūŹżŹ±£¬ÕāŃłµÄ”÷PACÓŠ¼øøö£æ
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©
£»£Ø2£©![]() £»£Ø3£©
£»£Ø3£©![]() £¬ÓŠ5øö£®
£¬ÓŠ5øö£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©Éč½»µćŹ½ĪŖy=a£Øx+1£©£Øx-3£©£¬Č»ŗó°ŃCµć×ų±ź“śČėĒó³öa¼“æÉ£»
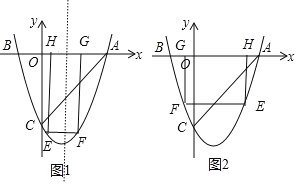
£Ø2£©ÉčE£Øt£¬t2-2t-3£©£¬ĢÖĀŪ£ŗµ±0<t<1Ź±£¬ČēĶ¼1£¬EF=2£Ø1-t£©£¬EH=-£Øt2-2t-3£©£¬ĄūÓĆÕż·½ŠĪµÄŠŌÖŹµĆ2£Ø1-t£©=-£Øt2-2t-3£©£»µ±1<t<3Ź±£¬ČēĶ¼2£¬ĄūÓĆÕż·½ŠĪµÄŠŌÖŹµĆ2£Øt-1£©=-£Øt2-2t-3£©£¬µ±t>3Ź±£¬2£Øt-1£©=t2-2t-3£¬Č»ŗó·Ö±š½ā·½³ĢµĆµ½Āś×ćĢõ¼žµÄtµÄÖµ£¬ŌŁ¼ĘĖć³ö¶ŌÓ¦µÄÕż·½ŠĪµÄ±ß³¤£»
£Ø3£©ÉčP£Øx£¬x2-2x-3£©£¬ĢÖĀŪ£ŗµ±-1<x<0Ź±£¬ÓÉÓŚS”÷ABC=6£¬Ōņ0<S”÷APC<6£¬µ±0<x<3Ź±£¬×÷PM”ĪyÖį½»ACÓŚµćM£¬ČēĶ¼3£¬Ēó³öÖ±ĻßACµÄ½āĪöŹ½ĪŖy=x-3£¬ŌņM£Øx£¬x-3£©£¬ĄūÓĆČż½ĒŠĪĆ껿¹«Ź½µĆS”÷APC=![]() 3£Ø-x2+3x£©£¬ĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹµĆ0<S”÷APC<
3£Ø-x2+3x£©£¬ĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹµĆ0<S”÷APC<![]() £¬ĖłŅŌ0<S”÷APC<6£¬ÓŚŹĒµĆµ½”÷PACĆ껿ĪŖÕūŹżŹ±£¬ĖüµÄÖµĪŖ1”¢2”¢3”¢4”¢5£®
£¬ĖłŅŌ0<S”÷APC<6£¬ÓŚŹĒµĆµ½”÷PACĆ껿ĪŖÕūŹżŹ±£¬ĖüµÄÖµĪŖ1”¢2”¢3”¢4”¢5£®
ŹŌĢā½āĪö£ŗ(1)ÉčÅ×ĪļĻß½āĪöŹ½ĪŖy=a(x+1)(x3)£¬
°ŃC(0,3)“śČėµĆ3a=3£¬½āµĆa=1£¬
ĖłŅŌÅ×ĪļĻß½āĪöŹ½ĪŖy=(x+1)(x3)£¬
¼“y=x22x3£»
(2)Å×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx=1£¬
ÉčE(t,t22t3)£¬
µ±0<t<1Ź±,ČēĶ¼1,EF=2(1t),EH=(t22t3)£¬
”ß¾ŲŠĪEFGHĪŖÕż·½ŠĪ£¬
”ąEF=EH,¼“2(1t)=(t22t3)£¬
ÕūĄķµĆt24t1=0,½āµĆt1=2+![]() (ÉįČ„),t2=2
(ÉįČ„),t2=2![]() (ÉįČ„)£»
(ÉįČ„)£»
µ±1<t<3Ź±,ČēĶ¼2,EF=2(t1),EH=(t22t3)£¬
”ß¾ŲŠĪEFGHĪŖÕż·½ŠĪ£¬
”ąEF=EH,¼“2(t1)=(t22t3)£¬
ÕūĄķµĆt25=0,½āµĆt1=![]() ,t2=
,t2=![]() (ÉįČ„)£¬
(ÉįČ„)£¬
“ĖŹ±Õż·½ŠĪEFGHµÄ±ß³¤ĪŖ2![]() 2£»
2£»
µ±t>3Ź±,EF=2(t1),EH=t22t3,
”ß¾ŲŠĪEFGHĪŖÕż·½ŠĪ£¬
”ąEF=EH,¼“2(t1)=t22t3£¬
ÕūĄķµĆt24t1=0,½āµĆt1=2+![]() ,t2=2
,t2=2![]() (ÉįČ„)£¬
(ÉįČ„)£¬
“ĖŹ±Õż·½ŠĪEFGHµÄ±ß³¤ĪŖ2![]() +2£¬
+2£¬
×ŪÉĻĖłŹöÕż·½ŠĪEFGHµÄ±ß³¤ĪŖ2![]() 2»ņ2
2»ņ2![]() +2£»
+2£»
(3)ÉčP(x,x22x3)£¬
µ±1<x<0Ź±£¬
”ßS”÷ABC=![]() ”Į4”Į3=6£¬
”Į4”Į3=6£¬
”ą0<S”÷APC<6£¬
µ±0<x<3Ź±,×÷PM”ĪyÖį½»ACÓŚµćM£¬ČēĶ¼3£¬
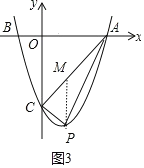
Ņ×µĆÖ±ĻßACµÄ½āĪöŹ½ĪŖy=x3,ŌņM(x,x3)£¬
”ąPM=x3(x22x3)=x2+3x£¬
”ąS”÷APC=![]() ”Į3(x2+3x)=
”Į3(x2+3x)=![]() x2+
x2+![]() x=
x=![]() (x
(x![]() )2+
)2+![]() £¬
£¬
µ±x=![]() Ź±,S”÷APCµÄĆ껿µÄ×ī“óÖµĪŖ
Ź±,S”÷APCµÄĆ껿µÄ×ī“óÖµĪŖ![]() ,¼“0<S”÷APC<
,¼“0<S”÷APC<![]() £¬
£¬
×ŪÉĻĖłŹö,0<S”÷APC<6£¬
”ą”÷PACĆ껿ĪŖÕūŹżŹ±£¬ĖüµÄÖµĪŖ1”¢2”¢3”¢4”¢5£¬¼“”÷PACÓŠ5øö.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹Ū²ģĻĀĮŠµČŹ½£¬²¢Ģ½¾æ
¢Ł![]()
¢Ś![]()
¢Ū![]()
””
£Ø1£©Š“³öµŚ¢ÜøöµČŹ½£ŗ______£»
£Ø2£©Ä³Ķ¬Ń§·¢ĻÖ£¬ĖÄøöĮ¬Šų×ŌČ»ŹżµÄ»ż¼ÓÉĻ1ŗ󣬽į¹ū¶¼½«ŹĒijŅ»øöÕūŹżµÄĘ½·½£®µ±ÕāĖÄøöŹż½Ļ“óŹ±æÉŅŌ½ųŠŠ¼ņ±ć¼ĘĖć£¬Čē£ŗ
![]() £®
£®
ĒėÄć²ĀĻėŠ“³öµŚnøöµČŹ½£¬ÓĆŗ¬ÓŠnµÄ“śŹżŹ½±ķŹ¾£¬²¢Ķعż¼ĘĖćŃéÖ¤ÄćµÄ²ĀĻė£®
£Ø3£©ČĪŗĪŹµŹżµÄĘ½·½¶¼ŹĒ·ĒøŗŹż£Ø¼“![]() £©£¬Ņ»øö·ĒøŗŹżÓėŅ»øöÕżŹżµÄŗĶ±Ų¶ØŹĒŅ»øöÕżŹż£Ø¼“
£©£¬Ņ»øö·ĒøŗŹżÓėŅ»øöÕżŹżµÄŗĶ±Ų¶ØŹĒŅ»øöÕżŹż£Ø¼“![]() Ź±£¬
Ź±£¬![]() £©£®øł¾ŻŅŌÉĻµÄ¹ęĀÉŗĶ·½·ØŹŌĖµĆ÷£ŗĪŽĀŪxĪŖŹ²Ć“ŹµŹż£¬¶ąĻīŹ½
£©£®øł¾ŻŅŌÉĻµÄ¹ęĀÉŗĶ·½·ØŹŌĖµĆ÷£ŗĪŽĀŪxĪŖŹ²Ć“ŹµŹż£¬¶ąĻīŹ½![]() µÄÖµÓĄŌ¶¶¼ŹĒÕżŹż£®
µÄÖµÓĄŌ¶¶¼ŹĒÕżŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖijŹŠ2016ÄźĘóŅµÓĆĖ®Įæx£Ø¶Ö£©ÓėøĆŌĀÓ¦½»µÄĖ®·Ńy£ØŌŖ£©Ö®¼äµÄŗÆŹż¹ŲĻµČēĶ¼£®

£Ø1£©µ±x”Ż50Ź±£¬Ēóy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ČōijĘóŅµ2016Äź10ŌĀ·ŻµÄĖ®·ŃĪŖ620ŌŖ£¬ĒóøĆĘóŅµ2016Äź10ŌĀ·ŻµÄÓĆĖ®Į棻
£Ø3£©ĪŖ¹ÄĄųĘóŅµ½ŚŌ¼ÓĆĖ®£¬øĆŹŠ×Ō2017Äź1ŌĀæŖŹ¼¶ŌŌĀÓĆĖ®Į泬¹ż80¶ÖµÄĘóŅµ¼ÓŹÕĪŪĖ®“¦Ąķ·Ń£¬¹ę¶Ø£ŗČōĘóŅµŌĀÓĆĖ®Įæx³¬¹ż80¶Ö£¬Ōņ³ż°“2016ÄźŹÕ·Ń±ź×¼ŹÕČ”Ė®·ŃĶā£¬³¬¹ż80¶ÖµÄ²æ·ÖĆæ¶ÖĮķ¼ÓŹÕ![]() ŌŖµÄĪŪĖ®“¦Ąķ·Ń£¬ČōijĘóŅµ2017Äź3ŌĀ·ŻµÄĖ®·ŃŗĶĪŪĖ®“¦Ąķ·Ń¹²600ŌŖ£¬ĒóÕāøöĘóŅµ3ŌĀ·ŻµÄÓĆĖ®Į森
ŌŖµÄĪŪĖ®“¦Ąķ·Ń£¬ČōijĘóŅµ2017Äź3ŌĀ·ŻµÄĖ®·ŃŗĶĪŪĖ®“¦Ąķ·Ń¹²600ŌŖ£¬ĒóÕāøöĘóŅµ3ŌĀ·ŻµÄÓĆĖ®Į森
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
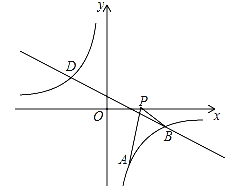
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćA£Ø1£¬a£©ŹĒ·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóÉĻŅ»µć£¬Ö±Ļß
µÄĶ¼ĻóÉĻŅ»µć£¬Ö±Ļß![]() Óė·“±ČĄżŗÆŹż
Óė·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóµÄ½»µćĪŖµćB”¢D£¬ĒŅB£Ø3£¬©1£©£¬Ēó£ŗ
µÄĶ¼ĻóµÄ½»µćĪŖµćB”¢D£¬ĒŅB£Ø3£¬©1£©£¬Ēó£ŗ
£Ø1£©Ē󷓱ȥżŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ĒóµćD×ų±ź£¬²¢Ö±½ÓŠ“³öy1£¾y2Ź±xµÄȔֵ·¶Ī§£»
£Ø3£©¶ÆµćP£Øx£¬0£©ŌŚxÖįµÄÕż°ėÖįÉĻŌĖ¶Æ£¬µ±Ļ߶ĪPAÓėĻ߶ĪPBÖ®²ī“ļµ½×ī“óŹ±£¬ĒóµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢµźĻśŹŪŅ»ÖÖĻśŹŪ³É±¾ĪŖĆæĒ§æĖ30ŌŖµÄĖ®²śĘ·£¬¾ŻŹŠ³”·ÖĪö£¬Čō°“ĆæĒ§æĖ40ŌŖĻśŹŪ£¬Ņ»øöŌĀÄÜŹŪ³ö500Ē§æĖ£»ĻśŹŪµ„¼ŪĆæÕĒ1ŌŖ£¬ŌĀĻśŹŪĮæ¾Ķ¼õÉŁ10Ē§æĖ£¬Õė¶ŌÕāÖÖĒéæö£¬Ēė½ā“šŅŌĻĀĪŹĢā£ŗ
£Ø1£©µ±ĻśŹŪµ„¼Ū¶ØĪŖĆæĒ§æĖ45ŌŖŹ±£¬¼ĘĖćŌĀĻśŹŪĮæŗĶŌĀĻśŹŪĄūČó£»
£Ø2£©øĆÉĢµźĻėŌŚŌĀĻśŹŪ³É±¾²»³¬¹ż10000ŌŖµÄĒéæöĻĀ£¬Ź¹µĆŌĀĻśŹŪĄūČó“ļµ½8000ŌŖ£¬ĻśŹŪµ„¼ŪÓ¦¶ØĪŖ¶ąÉŁ?
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ńÄźČėĻÄŅŌĄ“£¬ÓÉÓŚ³ÖŠų±©Óź£¬Ä³ĻŲŌāŹÜŃĻÖŲŗéĄŌŌÖŗ¦£¬ČŗÖŚ¶ŁŹ§¼ŅŌ°”£øĆĻŲĆńÕž¾ÖĪŖ½ā¾öČŗÖŚĄ§ÄŃ£¬ ½ō¼±×éÖÆĮĖŅ»Åś¾ČŌÖÕŹÅńŗĶŹ³Ę·×¼±øĖĶµ½ŌÖĒų”£ŅŃÖŖÕāÅśĪļ׏֊£¬ÕŹÅńŗĶŹ³Ę·¹² 640 ¼ž£¬ĒŅÕŹÅń±ČŹ³ Ę·¶ą 160 ¼ž”£
£Ø1£©ÕŹÅńŗĶŹ³Ę·ø÷ÓŠ¶ąÉŁ¼ž£æ
£Ø2£©ĻÖ¼Ę»®×āÓĆ A”¢B Į½ÖÖ»õ³µ¹² 16 Į¾£¬Ņ»“ĪŠŌ½«ÕāÅśĪļ׏ĖĶµ½ČŗÖŚŹÖÖŠ£¬ŅŃÖŖ A ÖÖ»õ³µæÉ×°ÕŹÅī40 ¼žŗĶŹ³Ę· 10 ¼ž£¬B ÖÖ»õ³µæÉ×°ÕŹÅń 20 ¼žŗĶŹ³Ę· 20 ¼ž£¬ŹŌĶعż¼ĘĖć°ļÖśĆńÕž¾ÖÉč¼Ę¼øÖÖŌĖŹä ·½°ø£æ
£Ø3£©ŌŚ£Ø2£©Ģõ¼žĻĀ£¬A ÖÖ»õ ³µĆæĮ¾Ščø¶ŌĖ·Ń 800 ŌŖ£¬B ÖÖ»õ³µĆæĮ¾Ščø¶ŌĖ·Ń 720 ŌŖ£¬ĆńÕž¾ÖӦєŌń ÄÄÖÖ·½°ø£¬²ÅÄÜŹ¹ŌĖŹä·ŃÓĆ×īÉŁ£æ×īÉŁ·ŃÓĆŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»Į¾Ęū³µ“ÓAµŲŹ»ĶłBµŲ£¬Ē°![]() Ā·¶ĪĪŖĘÕĶع«Ā·£¬ĘäÓąĀ·¶ĪĪŖøßĖŁ¹«Ā·.ŅŃÖŖĘū³µŌŚĘÕĶع«Ā·ÉĻŠŠŹ»µÄĖŁ¶ČĪŖ60km/h£¬ŌŚøßĖŁ¹«Ā·ÉĻŠŠŹ»µÄĖŁ¶ČĪŖ100km/h£¬Ęū³µ“ÓAµŲµ½BµŲŅ»¹²ŠŠŹ»ĮĖ2.2h.
Ā·¶ĪĪŖĘÕĶع«Ā·£¬ĘäÓąĀ·¶ĪĪŖøßĖŁ¹«Ā·.ŅŃÖŖĘū³µŌŚĘÕĶع«Ā·ÉĻŠŠŹ»µÄĖŁ¶ČĪŖ60km/h£¬ŌŚøßĖŁ¹«Ā·ÉĻŠŠŹ»µÄĖŁ¶ČĪŖ100km/h£¬Ęū³µ“ÓAµŲµ½BµŲŅ»¹²ŠŠŹ»ĮĖ2.2h.
ĒėÄćøł¾ŻŅŌÉĻŠÅĻ¢£¬¾ĶøĆĘū³µŠŠŹ»µÄ”°Ā·³Ģ”±»ņ”°Ź±¼ä”±£¬Ģį³öŅ»øöÓĆŅ»ŌŖŅ»“Ī·½³Ģ½ā¾öµÄĪŹĢā£¬²¢Š“³ö½ā“š¹ż³Ģ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼![]() £¬¾ŲŠĪ
£¬¾ŲŠĪ![]() µÄĮ½Ģõ±ß
µÄĮ½Ģõ±ß![]() ·Ö±šŌŚ
·Ö±šŌŚ![]() ÖįŗĶ
ÖįŗĶ![]() ÖįÉĻ£¬ŅŃÖŖµć
ÖįÉĻ£¬ŅŃÖŖµć![]() ”¢µć
”¢µć![]() .
.
(1)Čō°Ń¾ŲŠĪ![]() ŃŲÖ±Ļß
ŃŲÖ±Ļß![]() ÕŪµž£¬Ź¹µć
ÕŪµž£¬Ź¹µć![]() ĀäŌŚµć
ĀäŌŚµć![]() “¦£¬Ö±Ļß
“¦£¬Ö±Ļß![]() Óė
Óė![]() µÄ½»µć·Ö±šĪŖ
µÄ½»µć·Ö±šĪŖ![]() £¬ĒóÕŪŗŪ
£¬ĒóÕŪŗŪ![]() µÄ³¤£»
µÄ³¤£»
(2)ŌŚ(1)µÄĢõ¼žĻĀ£¬µć![]() ŌŚ
ŌŚ![]() ÖįÉĻ£¬ŌŚĘ½ĆęÄŚŹĒ·ń“ęŌŚµć
ÖįÉĻ£¬ŌŚĘ½ĆęÄŚŹĒ·ń“ęŌŚµć![]() £¬Ź¹ŅŌ
£¬Ź¹ŅŌ![]() ĪŖ¶„µćµÄĖıߊĪŹĒĮāŠĪ£æČō“ęŌŚ£¬ŌņĒėĒó³öµć
ĪŖ¶„µćµÄĖıߊĪŹĒĮāŠĪ£æČō“ęŌŚ£¬ŌņĒėĒó³öµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
(3)ČēĶ¼![]() £¬Čō
£¬Čō![]() ĪŖ
ĪŖ![]() ±ßÉĻµÄŅ»¶Æµć£¬ŌŚ
±ßÉĻµÄŅ»¶Æµć£¬ŌŚ![]() ÉĻČ”Ņ»µć
ÉĻČ”Ņ»µć![]() £¬½«¾ŲŠĪ
£¬½«¾ŲŠĪ![]() Čʵć
Čʵć![]() Ė³Ź±ÕėŠż×ŖŅ»ÖÜ£¬ŌŚŠż×ŖµÄ¹ż³ĢÖŠ£¬
Ė³Ź±ÕėŠż×ŖŅ»ÖÜ£¬ŌŚŠż×ŖµÄ¹ż³ĢÖŠ£¬![]() µÄ¶ŌÓ¦µćĪŖ
µÄ¶ŌÓ¦µćĪŖ![]() £¬ĒėÖ±½ÓŠ“³ö
£¬ĒėÖ±½ÓŠ“³ö![]() µÄ×ī“óÖµŗĶ×īŠ”Öµ.
µÄ×ī“óÖµŗĶ×īŠ”Öµ.


²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ABCDÖŠ£¬AB=6£¬AD=9£¬”ĻBADµÄĘ½·ÖĻß½»BCÓŚµćE£¬½»DCµÄŃÓ³¤ĻßÓŚµćF£¬BG”ĶAEÓŚG£¬BG=
ABCDÖŠ£¬AB=6£¬AD=9£¬”ĻBADµÄĘ½·ÖĻß½»BCÓŚµćE£¬½»DCµÄŃÓ³¤ĻßÓŚµćF£¬BG”ĶAEÓŚG£¬BG=![]() £¬ŌņĢŻŠĪAECDµÄÖܳ¤ĪŖ£Ø £©
£¬ŌņĢŻŠĪAECDµÄÖܳ¤ĪŖ£Ø £©
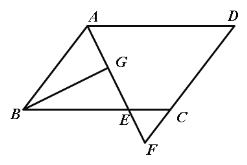
A£®22 B£®23 C£®24 D£®25
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com