
【题目】在等边△ABC中,AO是高,D为AO上一点,以CD为一边,在CD下方作等边△CDE,连接BE.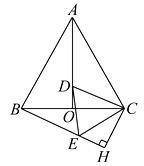
(1)求证:AD=BE;
(2)过点C作CH⊥BE,交BE的延长线于H,若BC=8,求CH的长.
【答案】
(1)证明:∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠ACD+∠BCD=∠ACB=60°,∠BCE+∠BCD=∠DCE=60°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
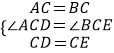 ,
,
∴△ACD≌△BCE(SAS);
∴AD=BE
(2)解:∵△ABC是等边三角形,AO是BC边上的高,
∴∠BAC=60°,且AO平分∠BAC,
∴∠CAD= ![]() ∠BAC=
∠BAC= ![]() ×60°=30°.
×60°=30°.
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∴∠CBE=30°.
又∵CH⊥BE,BC=8,
∴在Rt△BCH中,CH= ![]() BC=
BC= ![]() ×8=4,即CH=4
×8=4,即CH=4
【解析】(1)根据等边三角形的性质得出CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,从而得出∠ACD=∠BCE.然后利用SAS判断出△ACD≌△BCE ,根据全等三角形的性质得出AD=BE ;
(2)根据等腰三角形,底边上的三线合一得出∠CAD=30°.根据△ACD≌△BCE,得出∠CAD=∠CBE,从而得出∠CBE=30°.然后根据含30![]() 角的直角三角形的边角关系得出CH的长度。
角的直角三角形的边角关系得出CH的长度。


科目:初中数学 来源: 题型:
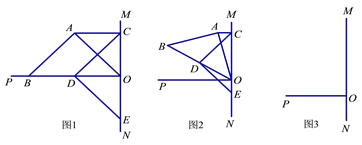
【题目】已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中, ![]() ,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
(1) 如图1,若点B在OP上,则①AC OE(填“<”,“=”或“>”);②线段CA、CO、CD满足的等量关系式是 ;
(2) 将图1中的等腰Rt△ABO绕O点顺时针旋转(![]() ),如图2,那么(1)中的结论②是否成立?请说明理由;
),如图2,那么(1)中的结论②是否成立?请说明理由;
(3) 将图1中的等腰Rt△ABO绕O点顺时针旋转(),请你在图3中画出图形,并直接写出线段CA、CO、CD满足的等量关系式 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市前年PM2.5的年均浓度为50微克/立方米,去年比前年下降了10%,如果今年PM2.5的年均浓度比去年也下降10%,那么今年PM2.5的年均浓度将是微克/立方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ ABC 的周长为 21,底边 BC=5,AB 的垂直平分线 DE 交 AB 于点 D,交 AC于点 E,则△BEC 的周长为( )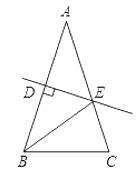
A.13
B.14
C.15
D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com