
【题目】(1)如图1,在△ABC中,∠A![]() ,P是BC边上的一点,
,P是BC边上的一点,![]() ,
,![]() 是点P关于AB、AC的对称点,连结
是点P关于AB、AC的对称点,连结![]() ,分别交AB、AC于点D、E.
,分别交AB、AC于点D、E.
①若![]() ,求
,求![]() 的度数;
的度数;
②请直接写出∠A与![]() 的数量关系:___________________________;
的数量关系:___________________________;
(2)如图2,在△ABC中,若∠BAC![]() ,用三角板作出点P关于AB、AC的对称点
,用三角板作出点P关于AB、AC的对称点![]() 、
、![]() ,(不写作法,保留作图痕迹),试判断点
,(不写作法,保留作图痕迹),试判断点![]() ,
,![]() 与点A是否在同一直线上,并说明理由.
与点A是否在同一直线上,并说明理由.


【答案】(1)64°;(2)∠DPE=180°-2∠A;(3)在.
【解析】(1)①由轴对称的性质以及四边形内角和为360°可得:∠DPP1+∠DPE+∠EPP2+∠A=180°(i),由三角形外角的性质以及三角形内角和为180°得到2∠DPP1+∠DPE+2∠EPP2=180°(ii),解方程组即可得到结论![]()
(2)由①得∠DPP1+∠DPE+∠EPP2+∠A=180°(i),2∠DPP1+∠DPE+2∠EPP2=180° (ii),解方程组即可得到结论.
(3)连接AP、AP1、AP2.根据轴对称的性质,可得:∠4=∠1,∠3=∠2, 由∠BAC=90°,得到∠3+∠4=90°,即有∠1+∠2+∠3+∠4=180°,从而得到结论.
(1)①∵点P、点P1关于直线AB对称,点P、点P2关于直线AC对称,∴PD=P1D,PE=P2E,∴∠P1=∠DPP1,∠P2=∠EPP2,∴∠EDP=2∠DPP1,∠DEP=2∠EPP2,∠DPP1+∠DPE+∠EPP2+∠A=180°(i)
∵2∠DPP1+∠DPE+2∠EPP2=180° (ii)
(ii)—(i)得:∠DPP1+∠EPP2=∠A,
又∵∠A=58°,∴∠DPP1+∠EPP2=58°,
∴∠DPE=64°![]()
(2)∠DPE=180°-2∠A .理由如下:
由①得:∠DPP1+∠DPE+∠EPP2+∠A=180°(i)
2∠DPP1+∠DPE+2∠EPP2=180° (ii)
(i)×2-(ii)得:2∠A-∠DPE=180°,
∴∠DPE=180°-2∠A .
(3)点P1,A,P2在同一条直线上.理由如下:
连接AP、AP1、AP2.
根据轴对称的性质,可得:∠4=∠1,∠3=∠2,

∵∠BAC=90°,即∠1+∠2=90°,
∴∠3+∠4=90°,
∴∠1+∠2+∠3+∠4=180°,
即∠P1AP2=180°,
∴点P1 、A、P2在同一条直线上.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿.其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何.”
译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?结合你学过的知识,解决下列问题:
(1)若设公鸡有x只,母鸡有y只,
①则小鸡有______只,买小鸡一共花费______文钱;(用含x,y的式子表示)
②根据题意列出一个含有x,y的方程:______;
(2)若对“百鸡问题”增加一个条件:公鸡数量是母鸡数量的3倍,求此时公鸡、母鸡、小鸡各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形ABCD中,AB=CD=7cm,AD=BC=5cm,∠A=∠B=∠C=∠D=90°,点E在线段AB上以lcms的速度由点A向点B运动,与此同时点F在线段BC上由点B向点C运动,设运动的时间均为ts.
(1)若点F的运动速度与点E的运动速度相等,当t=2时:
①判断△BEF与△ADE是否全等?并说明理由;
②求∠EDF的度数.
(2)如图2,将图1中的“长方形ABCD”改为“梯形ABCD”,且∠A=∠B=70°,AB=7cm,AD=BC=5cm,其他条件不变.设点F的运动速度为xcm/s.是否存在x的值,使得△BEF与△ADE全等?若存在,直接写出相应的x及t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个8×10的网格,每个小正方形的顶点叫格点,每个小正方形的边长均为1,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的图形△![]() .
.
(2)画出△ABC关于点O的中心对称图形 △![]() .
.
(3)△![]() 与△
与△![]() 组成的图形__________ 轴对称图形. (填“是”或“不是”)
组成的图形__________ 轴对称图形. (填“是”或“不是”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]()
![]() 交于A点,且点A的横坐标是4.双曲线
交于A点,且点A的横坐标是4.双曲线![]()
![]() 上有一动点C(m,n),
上有一动点C(m,n), ![]() .过点A作
.过点A作![]() 轴垂线,垂足为B,过点C作
轴垂线,垂足为B,过点C作![]() 轴垂线,垂足为D,联结OC.
轴垂线,垂足为D,联结OC.

(1)求![]() 的值;
的值;
(2)设![]() 的重合部分的面积为S,求S与m的函数关系;
的重合部分的面积为S,求S与m的函数关系;
(3)联结AC,当第(2)问中S的值为1时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
(解析)解:BE∥DF.
∵AB⊥BC,
∴∠ABC= °,
即∠3+∠4= °.
又∵∠1+∠2=90°,
且∠2=∠3,
∴ = .
理由是: .
∴BE∥DF.
理由是: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月30日上午符离大道正式开通,同时宿州至徐州的K902路城际公交开通试运营,小明先乘K902路城际公交车到五柳站下车,再步行到五柳景区游玩,从出发地到五柳景区全程31千米,共用了1个小时,已知步行的速度每小时4千米,K902路城际公交的速度是步行速度的10倍,求小明乘公交车所行驶的路程和步行的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
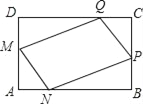
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于440平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com