
【题目】如图,在□ABCD中,对角线AC、BD交于点O,过点O的直线分别交BC、AD于F、E.若AD=6cm,AB=4cm,OE=2cm,则梯形EFCD的周长是( )
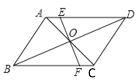
A.16cmB.15cmC.14cmD.12cm
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
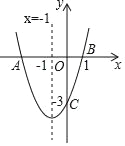
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
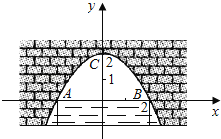
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.

(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足![]() ,
,![]()
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
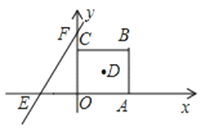
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时生产一种零件,在5天中,两台机床每天出次品的数量如下表:
甲 | 0 | 1 | 2 | 0 | 2 |
乙 | 2 | 1 | 0 | 1 | 1 |
关于以上数据的平均数、中位数、众数和方差,说法不正确的是
A. 甲、乙的平均数相等B. 甲、乙的众数相等
C. 甲、乙的中位数相等D. 甲的方差大于乙的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当三角形中一个内角![]() 是另一个内角
是另一个内角![]() 的2倍时,则称此三角形为“倍角三角形”,其中角
的2倍时,则称此三角形为“倍角三角形”,其中角![]() 称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是________________.
称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com