
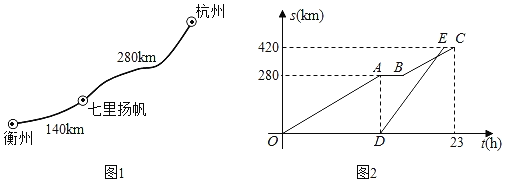
【题目】2020年5月16日,“钱塘江诗路”航道全线开通,一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h,游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变).
(1)写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.
(2)若货轮比游轮早36分钟到达衢州.问:
①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?
【答案】(1)从杭州出发前往衢州共用了23h.2h;(2)①货轮出发后8小时追上游轮;②21.6h或22.4h时游轮与货轮何时相距12km
【解析】
(1)根据图中信息解答即可.
(2)①求出B,C,D,E的坐标,利用待定系数法求解即可.
(3)分两种情形分别构建方程求解即可.
解:(1)C点横坐标的实际意义是游轮从杭州出发前往衢州共用了23h.
∴游轮在“七里扬帆”停靠的时长=23﹣(420÷20)=23﹣21=2(h).
(2)①280÷20=14h,
∴点A(14,280),点B(16,280),
∵36÷60=0.6(h),23﹣0.6=22.4,
∴点E(22.4,420),
设BC的解析式为s=20t+b,把B(16,280)代入s=20t+b,可得b=﹣40,
∴s=20t﹣40(16≤t≤23),
同理由D(14,0),E(22,4,420)可得DE的解析式为s=50t﹣700(14≤t≤22.4),
由题意:20t﹣40=50t﹣700,
解得t=22,
∵22﹣14=8(h),
∴货轮出发后8小时追上游轮.
②相遇之前相距12km时,20t﹣4﹣(50t﹣700)=12,解得t=21.6.
相遇之后相距12km时,50t﹣700﹣(20t﹣40)=12,解得t=22.4,
∴21.6h或22.4h时游轮与货轮何时相距12km.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:

(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=2![]() ,BC=8,按下列步骤作图:
,BC=8,按下列步骤作图:
①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于![]() EF的长为半径作弧相交于点H,作射线AH;
EF的长为半径作弧相交于点H,作射线AH;
②分别以点A,B为圆心,大于![]() AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;
AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;
③以点O为圆心,线段OA长为半径作圆.
则⊙O的半径为( )
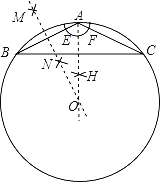
A.2![]() B.10C.4D.5
B.10C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
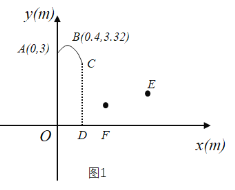
【题目】在篮球比赛中,东东投出的球在点A处反弹,反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系),抛物线顶点为点B.
(1)求该抛物线的函数表达式.
(2)当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m.
①求OD的长.
②东东抢到球后,因遭对方防守无法投篮,他在点D处垂直起跳传球,想将球沿直线快速传给队友华华,目标为华华的接球点E(4,1.3).东东起跳后所持球离地面高度h1(m)(传球前)与东东起跳后时间t(s)满足函数关系式h1=﹣2(t﹣0.5)2+2.7(0≤t≤1);小戴在点F(1.5,0)处拦截,他比东东晚0.3s垂直起跳,其拦截高度h2(m)与东东起跳后时间t(s)的函数关系如图2所示(其中两条抛物线的形状相同).东东的直线传球能否越过小戴的拦截传到点E?若能,东东应在起跳后什么时间范围内传球?若不能,请说明理由(直线传球过程中球运动时间忽略不计).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,一个三角尺的直角顶点与
,一个三角尺的直角顶点与![]() 边的中点
边的中点![]() 重合,且两条直角边分别经过点
重合,且两条直角边分别经过点![]() 和点
和点![]() ,将三角尺绕点
,将三角尺绕点![]() 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与
按顺时针方向旋转任意一个锐角,当三角尺的两直角边与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() 时,下列结论中错误的是( )
时,下列结论中错误的是( )
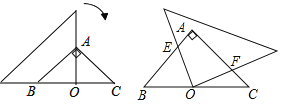
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
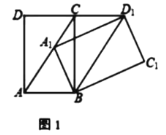
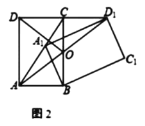
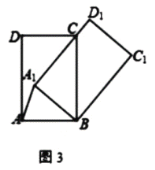
【题目】将矩形![]() 绕点
绕点![]() 顺时针旋转得到矩形
顺时针旋转得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]()
(1)当点![]() 落在
落在![]() 上时
上时
①如图1,若![]() ,求证:
,求证:![]()
②如图2,![]() 交
交![]() 于点
于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,
,
①如图3,当![]() 过点C时,则
过点C时,则![]() 的长=_____.
的长=_____.
②当![]() 时,作
时,作![]() ,
,![]() 绕点
绕点![]() 转动,当直线
转动,当直线![]() 经过
经过![]() 时,直线
时,直线![]() 交边
交边![]() 于
于![]() ,
,![]() 的值=______.
的值=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其余两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,每平方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.
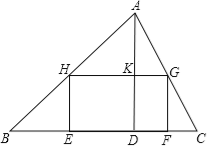
(1)当FG长为多少米时,种草的面积与种花的面积相等?
(2)当矩形EFGH的边FG为多少米时,△ABC空地改造总投资最小,最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
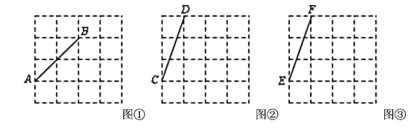
【题目】图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求长写出画法.
均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求长写出画法.
(1)在图①中以线段![]() 为边画一个直角△
为边画一个直角△![]() ;
;
(2)在图②中以线段![]() 为边画一个轴对称△
为边画一个轴对称△![]() ,使其面积为5;
,使其面积为5;
(3)在图③中以线段![]() 为边画一个轴对称四边形
为边画一个轴对称四边形![]() ,使其面积为6.
,使其面积为6.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com