
【题目】在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E. 
(1)若∠ABE=38°,求∠EBC的度数;
(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.
【答案】
(1)解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=38°,
∵AB=AC,
∴∠ABC=∠C= ![]() =71°,
=71°,
∴∠EBC=∠ABC﹣∠ABE=71°﹣38°=33°
(2)解:当BC=13cm时,AB=AC=11.5cm,
∵AE=BE,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=13cm+11.5cm=24.5cm;
当AB=AC=13cm时,则BC=10cm,
∵AE=BE,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=10cm+13cm=23cm;
即△BCE的周长为24.5cm或23cm
【解析】(1)由DE是AB的垂直平分线,根据线段垂直平分线的性质得出AE=BE,则可求得∠ABE的度数,又由AB=AC,根据等边对等角与三角形内角和定理,即可求得∠ABC的度数,继而求得答案;(2)求出AC和BC的值,再根据线段垂直平分线的性质得出AE=BE,求出△BCE的周长=AC+BC,代入求出即可.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图1,小明将一张长为4、宽为3的矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用点F表示).
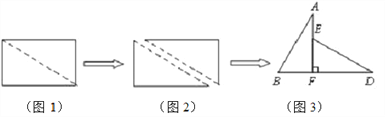
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
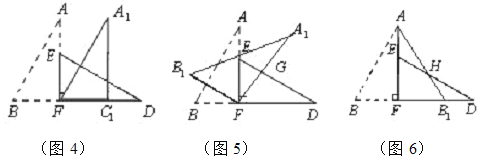
(1)将图3中的△ABF沿BD向右平移到图4中![]() 的位置,其中点B与点F 重合,请你求出平移的距离 ;
的位置,其中点B与点F 重合,请你求出平移的距离 ;
(2)在图5中若∠GFD=60°,则图3中的△ABF绕点 按 方向旋转 到图5的位置;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,试问:△AEH和△HB1D的面积大小关系.说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y﹣z
C.x+2y﹣2z=x﹣2(z+y)
D.﹣a+c+d+b=﹣(a﹣b)﹣(﹣c﹣d)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点. 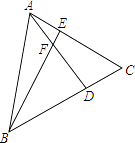
(1)求证:△ABE≌△CAD;
(2)当E、D运动时,∠BFD大小是否发生改变?若不变求其大小,若改变求其变化范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com