
分析 (1)根据题意易得新抛物线的顶点,根据顶点式及平移前后二次项的系数不变可得新抛物线的解析式.
(2)令y=0,则根据一元二次方程-2(x+1)2+6=0的根的判别式的符号来判断平移后的抛物线与x轴是否有公共点.
解答 解:(1)抛物线y=-2x2+4x+1=-2(x-1)2+3,
平移后,得y=-2(x-1+2)2+3+3=-2(x+1)2+6;
(2)令y=0,则-2(x+1)2+6=0,即x2+2x-2=0,
△=22-4×(-2)=12>0,
故平移后抛物线与x轴有2个公共点.
点评 本题考查了二次函数图象与几何变换,抛物线与x轴的交点.注意:抛物线平移不改变二次项的系数的值.


科目:初中数学 来源: 题型:解答题
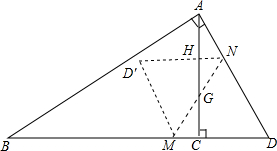 已知,Rt△ABD中,∠BAD=90°,∠D=60°,AC⊥BD,CD=1,N,M分别从D点同时出发,N从D点向A点运动,M从D点向B点运动,当其中一动点到达终点,另一点停止运动,N,M速度都为1.当运动时间为t时,连接MN,将△DMN沿MN翻折.得到△D′MN,并记△D′MN与△ACB重叠部分面积为S,求S与t之间的函数关系式.
已知,Rt△ABD中,∠BAD=90°,∠D=60°,AC⊥BD,CD=1,N,M分别从D点同时出发,N从D点向A点运动,M从D点向B点运动,当其中一动点到达终点,另一点停止运动,N,M速度都为1.当运动时间为t时,连接MN,将△DMN沿MN翻折.得到△D′MN,并记△D′MN与△ACB重叠部分面积为S,求S与t之间的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16.04×105 | B. | 1.6×106 | C. | 1.604×106 | D. | 0.1604×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将长方形纸片ABCD按如下顺序进行折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③);请你求出图②中∠BCB′的度数.
将长方形纸片ABCD按如下顺序进行折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③);请你求出图②中∠BCB′的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com