
【题目】已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为 . 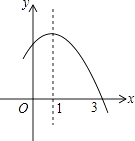
【答案】x1=﹣1或x2=3
【解析】解:依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线与x轴的另一个交点横坐标为1﹣(3﹣1)=﹣1,
∴交点坐标为(﹣1,0)
∴当x=﹣1或x=3时,函数值y=0,
即﹣x2+2x+m=0,
∴关于x的一元二次方程﹣x2+2x+m=0的解为x1=﹣1或x2=3.
所以答案是:x1=﹣1或x2=3.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=![]() 的图象经过D点.
的图象经过D点.

(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
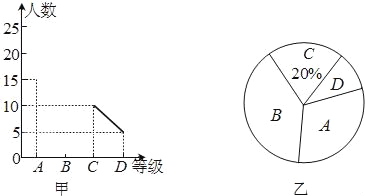
【题目】“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行),某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 100 | 250 | 450 |
(1)现在该公司收购了140吨蔬菜,如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工,剩余部分直接销售 |
获利(元) |
(2)如果先进行精加工,然后进行粗加工,要求15天刚好加工完140吨蔬菜,则应如何分配加工时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、C的坐标分别为(﹣1,0)、(0,﹣ ![]() ),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.
),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.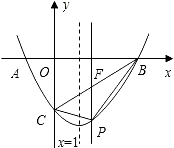
(1)求该二次函数的解析式;
(2)若设点P的横坐标为m,用含m的代数式表示线段PF的长;
(3)求△PBC面积的最大值,并求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A1B1C1是由三角形ABC平移后得到的,已知三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0-6,y0-2).
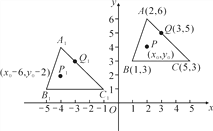
(1)已知A(2,6),B(1,3),C(5,3),Q(3,5),请写出A1,B1,C1,Q1的坐标;
(2)试说明三角形A1B1C1是如何由三角形ABC得到的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a=(﹣0.1)0 , b=(﹣0.1)﹣1 , c=(﹣ ![]() )﹣2 , 那么a,b,c的大小关系为( )
)﹣2 , 那么a,b,c的大小关系为( )
A.a>b>c
B.c>a>b
C.c>b>a
D.a>c>b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com