
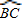 的长;
的长;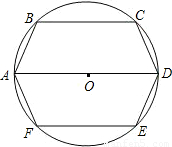
 (1)解:连接OB、OC,由∠BAD=75°,OA=OB知∠AOB=30°,
(1)解:连接OB、OC,由∠BAD=75°,OA=OB知∠AOB=30°, 的长为
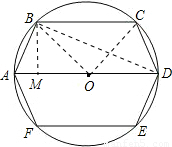
的长为 .(3分)
.(3分)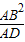 =
=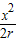 ,∴BC=2r-
,∴BC=2r-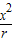 ,同理EF=2r-
,同理EF=2r-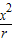 ,(8分)
,(8分)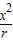 )=-
)=-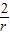 x2+4x+4r=-
x2+4x+4r=-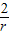 (x-r)2+6r,其中0<x<
(x-r)2+6r,其中0<x< ,(9分)
,(9分)

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:
如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com