练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若一元二次方程x2﹣2x+k=0有两个不相等的实数根，则k的取值范围是 ．

    【答案】k＜1
    【解析】解：∵一元二次方程x2﹣2x+k=0有两个不相等的实数根， ∴△=b2﹣4ac=4﹣4k＞0，
    解得：k＜1，
    则k的取值范围是：k＜1．
    所以答案是：k＜1．
    【考点精析】根据题目的已知条件，利用求根公式的相关知识可以得到问题的答案，需要掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如果水位升高3m时，水位变化记作+3m，那么水位下降5m时，水位变化记作：　 　 m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，抛物线经过A（﹣4，0），B（0，4）两点，与x轴交于另一点C，直线y=x+5与x轴交于点D，与y轴交于点E．

    （1）求抛物线的解析式；

    （2）点P是第二象限抛物线上的一个动点，连接EP，过点E作EP的垂线l，在l上截取线段EF，使EF=EP，且点F在第一象限，过点F作FM⊥x轴于点M，设点P的横坐标为t，线段FM的长度为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；

    （3）在（2）的条件下，过点E作EH⊥ED交MF的延长线于点H，连接DH，点G为DH的中点，当直线PG经过AC的中点Q时，求点F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

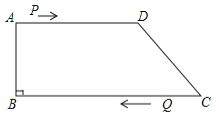
    【题目】如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C运动，点P从点A出发的同时点Q从点C出发，以1cm/s的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．

    （1）从运动开始，当t取何值时，PQ∥CD？

    （2）从运动开始，当t取何值时，△PQC为直角三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果收入15元记作+15元，那么支出20元记作元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求证：不论k为何值时，关于x的一元二次方程x2+（k﹣2）x+（k﹣4）＝0有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，AB=AC，AB的垂直平分线与直线AC相交所成锐角为40°，则此等腰三角形的顶角为（ ）
    A.50°
    B.60°
    C.150°
    D.50°或130°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．

    问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线经过B、C两点，顶点D在正方形内部．

    （1）直接写出点D（m，n）所有的特征线；

    （2）若点D有一条特征线是y=x+1，求此抛物线的解析式；

    （3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小王去早市为餐馆选购蔬菜，他指着标价为每斤3元的豆角问摊主：“这豆角能便宜吗？”摊主：“多买按八折，你要多少斤？”小王报了数量后摊主同意按八折卖给小王，并说：“之前一人只比你少买5斤就是按标价，还比你多花了3元呢！”小王购买豆角的数量是（　　）

    A. 30斤 B. 25斤 C. 20斤 D. 15斤

    查看答案和解析>>

    同步练习册答案