

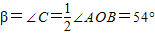 ;
;
 ∠AOB=
∠AOB= (180°-2α)=90°-α.
(180°-2α)=90°-α.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
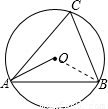
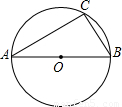
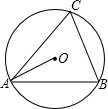 如图△ABC是⊙O内接三角形,点C是优孤AB上一点(点C与A、B不重合)设∠OAB=α,∠C=β.
如图△ABC是⊙O内接三角形,点C是优孤AB上一点(点C与A、B不重合)设∠OAB=α,∠C=β.查看答案和解析>>
科目:初中数学 来源:《第27章 圆(一)》2010年散水头中学单元检测(解析版) 题型:填空题
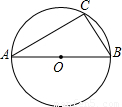
查看答案和解析>>
科目:初中数学 来源:2010-2011学年河北省唐山市玉田县散水头中学九年级(上)第一次月考数学试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009年安徽省巢湖市初中毕业班联考数学试卷(解析版) 题型:解答题
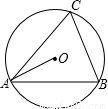
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com