
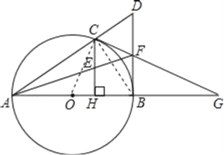
【题目】如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(1)求证:FC=FB;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.

【答案】(1)见解析;(2)见解析;(3)2![]()
【解析】
(1)连接OC,BC,证△AEC∽△AFD,△AHE∽△ABF,推出BF=DF,根据直角三角形斜边上中线性质得出CF=DF=BF即可.
(2)只要证明∠FCB=∠CAB即可推出CG是⊙O切线.
(2)由EF=FC,推出∠G=∠FAG,推出AF=FG,求出AB=BG,由切割线定理得出(2+FG)2=BG×AG=2BG2,在Rt△BFG中,由勾股定理得出BG2=FG2-BF2,推出FG2-4FG-12=0,求出FG即可,再在Rt△ABF中利用勾股定理即可解决问题.
(1)证明:连接OC,BC,
∵CH∥BD,
∴△AEC∽△AFD,△AHE∽△ABF,
∴![]()
![]()
∵CE=EH(E为CH中点),
∴BF=DF,
∵AB为⊙O的直径,
∴∠ACB=∠DCB=90°,
∵BF=DF,
∴CF=DF=BF(直角三角形斜边上的中线等于斜边的一半),
即CF=BF.
(2)证明∵BF切⊙O于B,
∴∠FBC=∠CAB,
∵OC=OA,CF=BF,
∴∠FCB=∠FBC,∠OCA=∠OAC,
∴∠FCB=∠CAB,
∵∠ACB=90°,
∴∠ACO+∠BCO=90°,
∴∠FCB+∠BCO=90°,
即OC⊥CG,
∴CG是⊙O切线,
(3)解:∵BF=CF=DF(已证),EF=BF=2,
∴EF=FC,
∴∠FCE=∠FEC,
∵∠AHE=∠CHG=90°,
∴∠FAH+∠AEH=90°,∠G+∠GCH=90°,
∵∠AEH=∠CEF,
∴∠G=∠FAG,
∴AF=FG,
∵FB⊥AG,
∴AB=BG,
∵GA是⊙O割线,AB=BG,FB=FE=2,
∴由切割线定理得:(2+FG)2=BG×AG=2BG2,
在Rt△BFG中,由勾股定理得:BG2=FG2﹣BF2,
∴FG2﹣4FG﹣12=0,
解得:FG=6,FG=﹣2(舍去),
由勾股定理得:
AB=BG=4![]() ,
,
∴⊙O的半径是2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.(直接填写答案)
(1)点A关于点O中心对称的点的坐标为 ;
(2)点A1的坐标为 ;
(3)在旋转过程中,点B经过的路径为弧BB1,那么弧BB1的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有5个分别标有数字1,2,3,4,5的小球,它们的形状、大小、质地等完全相同.雄威同学先从盒子里随机取出第一个小球,记下数字为x;不放回盒子,再由丽贤同学随机取出第二个小球,记下数字为y.
(1)请用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;
(2)求雄威同学、丽贤同学各取一个小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
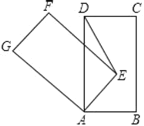
【题目】如图,将一个8cm×16cm智屏手机抽象成一个的矩形ABCD,其中AB=8cm,AD=16cm,然后将它围绕顶点A逆时针旋转一周,旋转过程中A、B、C、D的对应点依次为A、E、F、G,则当△ADE为直角三角形时,若旋转角为α(0<α<360°),则α的大小为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
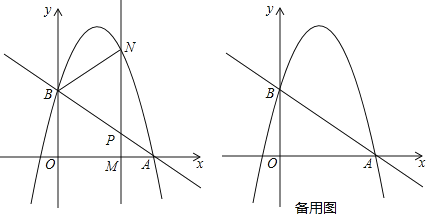
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过点A,B.
经过点A,B.
(1)求点B的坐标和抛物线的解析式;
(2)设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①求PN的最大值;
②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com