
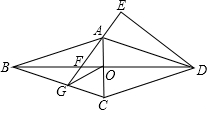
 如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC=2,BD=6,将△AOD沿AD翻折得到△AED,延长EA交BD于点F,交BC于点G.连接OG,则△FOG的面积是$\frac{9}{40}$.
如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC=2,BD=6,将△AOD沿AD翻折得到△AED,延长EA交BD于点F,交BC于点G.连接OG,则△FOG的面积是$\frac{9}{40}$. 分析 作AH⊥CD于H,GN⊥AC于N.思想利用勾股定理求出菱形的边长,根据菱形的两个面积公式求出AH,利用相似三角形求出GN、AN、OF即可解决问题.
解答 解: 作AH⊥CD于H,GN⊥AC于N.
作AH⊥CD于H,GN⊥AC于N.
∵四边形ABCD是菱形.
∴AC⊥BD,OA=OC=1,OB=OD=3,
∴CD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴$\frac{1}{2}$•AC•BD=CD•AH,
∴AH=$\frac{3}{5}$$\sqrt{10}$,DH=$\sqrt{A{D}^{2}-A{H}^{2}}$=$\frac{4}{5}$$\sqrt{10}$,
∵∠CAG+2∠DAC=180°,∠ADC+2∠DAC=180°,
∴∠CAG=∠ADC,
∵∠ACG=∠ACD=∠CAD,
∠AGC=∠ACG,
∴AG=AC=2,
∵∠ANG=∠AHD,
∴△AGN∽△DAH,
∴$\frac{GN}{AH}$=$\frac{AG}{AD}$=$\frac{AN}{DH}$,
∴GN=$\frac{6}{5}$,AN=$\frac{8}{5}$,
∵OF∥GN,
∴$\frac{OF}{GN}$=$\frac{AO}{AN}$,
∴OF=$\frac{3}{4}$,
∴S△OFG=$\frac{1}{2}$•OF•ON=$\frac{1}{2}$•$\frac{3}{4}$•$\frac{3}{5}$=$\frac{9}{40}$.
故答案为$\frac{9}{40}$.
点评 本题考查菱形的性质、翻折变换、勾股定理、相似三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
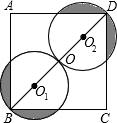 如图,在正方形ABCD中,AB=8,O为对角线BD的中点,分别以OB,OD为直径作⊙O1,⊙O2.
如图,在正方形ABCD中,AB=8,O为对角线BD的中点,分别以OB,OD为直径作⊙O1,⊙O2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,A是硬币周围上一点,硬币与数轴相切于原点O(A与O重合),假设硬币的直径为1个单位长度,若将硬币沿数轴方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是±π.(根据最新教材已作修改)
如图,A是硬币周围上一点,硬币与数轴相切于原点O(A与O重合),假设硬币的直径为1个单位长度,若将硬币沿数轴方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是±π.(根据最新教材已作修改)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
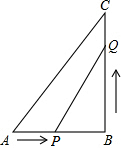 已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
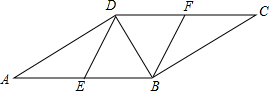 如图,在?ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
如图,在?ABCD中,E,F分别为边AB,CD的中点,BD是对角线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com