
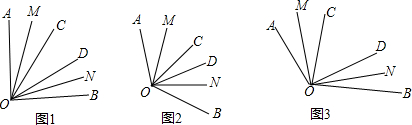
分析 根据角平分线的定义和图形中角与角之间的关系,推导出∠MON=$\frac{1}{2}$(∠AOB+∠COD),再代值即可.
解答 解:∵OM是∠AOC的角平分线,
∴∠COM=$\frac{1}{2}$∠AOC.
∵ON是∠BOD的角平分线,
∴∠DON=$\frac{1}{2}$∠BOD,
∴∠MON=∠COM+∠COD+∠DON
=$\frac{1}{2}$∠AOC+∠COD+$\frac{1}{2}$∠BOD
=$\frac{1}{2}$(∠AOC+∠BOD)+∠COD
=$\frac{1}{2}$(∠AOB-∠COD)+∠COD
=$\frac{1}{2}$∠AOB-$\frac{1}{2}$∠COD+∠COD
=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD
=$\frac{1}{2}$(∠AOB+∠COD)
①∵∠AOB=90°,∠COD=30°,
∴∠MON=$\frac{1}{2}$(∠AOB+∠COD)=$\frac{1}{2}$(90°+30°)=60°,
②∵∠AOB=120°,∠COD=20°,
∴∠MON=$\frac{1}{2}$(∠AOB+∠COD)=$\frac{1}{2}$(120°+20°)=140°,
②∵∠AOB=α°,∠COD=β°,
∴∠MON=$\frac{1}{2}$(∠AOB+∠COD)=$\frac{1}{2}$(α°+β°).
点评 此题是角平分线的定义,主要考查了角平分线的定义,识别图形中角与角的关系,找出图形中角之间的关系是解本题的关键,也是难点.


科目:初中数学 来源: 题型:选择题
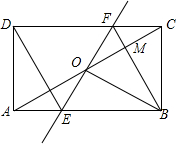 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
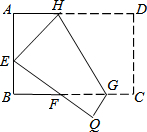 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是8cm.
如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是8cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-m}$ | B. | -$\sqrt{m}$ | C. | -$\sqrt{-m}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
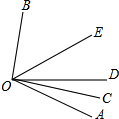 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
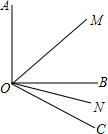 如图,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,
如图,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
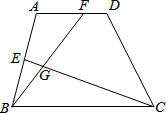 如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )
如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )| A. | 95 | B. | 100 | C. | 105 | D. | 110 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com