
【题目】在平面直角坐标系中,A(5,0),B(0,5).
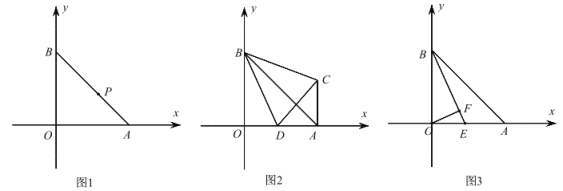
(1)如图 1,P 是 AB 上一点且![]()
![]() ,求 P 点坐标;
,求 P 点坐标;
(2)如图 2,D 为 OA 上一点,AC∥OB 且∠CBO=∠DCB,求∠CBD 的度数;
(3)如图 3,E 为 OA 上一点,OF⊥BE 于 F,若∠BEO=45°+∠EOF,求![]() 的值
的值
【答案】(1)(3,2) (2)45° (3)2
【解析】
(1)作PG⊥x轴于G,PN⊥y轴于N,根据相似三角形的性质列出比例式,分别求出PG,PN,得到P点坐标;
(2)作BG⊥AC交AC的延长线于G,作BH⊥CD于H,分别证明△BCH≌△BCG和Rt△BOD≌Rt△BHD,根据全等三角形的性质得到∠CBH=∠CBG,∠BOD=∠HOD,结合图形计算;
(3)根据题意和三角形内角和定理分别求出∠BEO=67.5°,∠EOF=22.5°,作∠BOP=∠OBE,设OF=a,根据三角形外角的性质,相似三角形的性质分别求出BF,EF,代入计算即可.
(1)作PG⊥x轴于G,PN⊥y轴于N,

∵![]()
![]()
∴![]()
∵A(5,0),B(0,5),
∴OA=5,OB=5,
∵PG⊥x轴,
∴PG∥OB,
∴△AGP∽△AOB,
∴![]() ,即
,即![]() ,
,
解得,PG=2,
同理,PN=3,
∴P点坐标为(3,2);
(2)作BG⊥AC交AC的延长线于G,作BH⊥CD于H,

∴四边形BOAG为矩形,
∴BO=BG,
∵OA=OB,
∴矩形BOAG为正方形,
∵AC∥OB
∴∠CBO=∠BCG,
∵∠CBO=∠DCB,
∴∠BCG=∠DCB,
在△BCH和△BCG中,
 ,
,
∴△BCH≌△BCG(AAS),
∴∠CBH=∠CBG,BG=BH,
∴BO=BH,
在Rt△BOD和Rt△BHD中,
![]()
∴Rt△BOD≌Rt△BHD(HL),
∴∠BOD=∠HOD,
∴∠CBD=∠DBH+∠CBH=![]() ∠OBG=45°;
∠OBG=45°;
(3)

∵∠BEO=45°+∠EOF,∠BEO+∠EOF=90°,
∴∠BEO=67.5°,∠EOF=22.5°,
则∠OBE=22.5°,
作∠BOP=∠OBE=22.5°,
则PB=PO,∠OPF=45°,
设OF=a,则PF=OF=a,由勾股定理得,OP=![]() a,
a,
∴PB=![]() a,
a,
∴BF=![]() a+a,
a+a,
∵∠BOP=∠OBE,∠OFB=∠EFO=90°,
∴△OFB∽△EFO,
∴EF=![]() a-a,
a-a,
∴


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=18,cosB=![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )

A. 6![]() B. 7
B. 7![]() C. 8
C. 8![]() D. 9
D. 9![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:
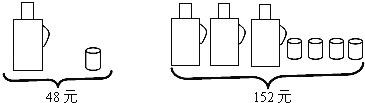
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你用树状图或列表法列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
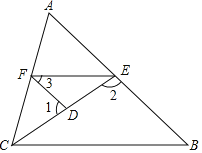
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B.
(1)求证:EF∥BC;
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芳芳妈对家里的经济收支情况有记帐的好习惯.下表记录的是她家2018年第一季度水表、电表的读表数和所缴水电费的情况:
时间(月份) | 水表读数(吨) | 电表读数(度) | 水电费(元) |
2018.1 | 528 | 1235 | 65 |
2018.2 | 538 | 1265 | 59 |
2018.3 | 558 | 1305 | 102 |
(1)请你根据表中提供的信息求出水、电的收费单价(即每吨水的收费标准和每度电的收费标准);
(2)今年4月份芳芳家水表读数为574(吨),电表读数为1340(度),那么芳芳家本月水电费应缴多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC=90![]() ,如果CD、CM分别是斜边上的高和中线,AC=2,BC=4,那么下列结论中错误的是( )
,如果CD、CM分别是斜边上的高和中线,AC=2,BC=4,那么下列结论中错误的是( )
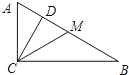
A. ∠ACD=∠BB. CM=![]() C. ∠B=30
C. ∠B=30![]() D. CD=
D. CD=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com