
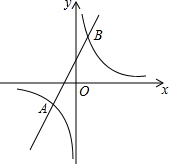
 如图,直线y=2x+4与反比例函数y=$\frac{k}{x}$的图象相交于A(-3,a)和B两点
如图,直线y=2x+4与反比例函数y=$\frac{k}{x}$的图象相交于A(-3,a)和B两点分析 (1)把点A(-3,a)代入y=2x+4与y=$\frac{k}{x}$即可得到结论;
(2)根据已知条件得到M($\frac{m+4}{2}$,m),N($\frac{6}{m}$,m),根据MN=4列方程即可得到结论;
(3)根据$\frac{6}{x-5}$>x得到$\frac{6-{x}^{2}+5x}{x-5}$>0解不等式组即可得到结论.
解答 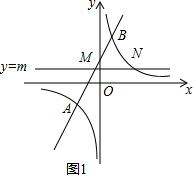 (1)∵点A(-3,a)在y=2x+4与y=$\frac{k}{x}$的图象上,
(1)∵点A(-3,a)在y=2x+4与y=$\frac{k}{x}$的图象上,
∴2×(-3)+4=a,
∴a=-2,
∴k=(-3)×(-2)=6;
(2)∵M在直线AB上,
∴M($\frac{m-4}{2}$,m),N在反比例函数y=$\frac{6}{x}$上,
∴N($\frac{6}{m}$,m),
∴MN=xN-xM=$\frac{6}{m}$-$\frac{m-4}{2}$=4或xM-xN=$\frac{m-4}{2}$-$\frac{6}{m}$=4,
解得:∵m>0,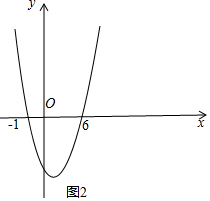
∴m=2或m=6+4$\sqrt{3}$;
(3)x<-1或5<x<6,
由$\frac{6}{x-5}$>x得:$\frac{6}{x-5}$-x>0,
∴$\frac{6-{x}^{2}+5x}{x-5}$>0,
∴$\frac{{x}^{2}-5x-6}{x-5}$<0,
∴$\left\{\begin{array}{l}{{x}^{2}-5x-6>0}\\{x-5<0}\end{array}\right.$或$\left\{\begin{array}{l}{{x}^{2}-5x-6<0}\\{x-5>0}\end{array}\right.$,
结合抛物线y=x2-5x-6的图象可知,由$\left\{\begin{array}{l}{{x}^{2}-5x-6>0}\\{x-5<0}\end{array}\right.$得
$\left\{\begin{array}{l}{x<-1或x>6}\\{x<5}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x<-1}\\{x<5}\end{array}\right.$或$\left\{\begin{array}{l}{x>6}\\{x<5}\end{array}\right.$,
∴此时x<-1,
由$\left\{\begin{array}{l}{{x}^{2}-5x-6<0}\\{x-5>0}\end{array}\right.$得,$\left\{\begin{array}{l}{-1<x<6}\\{x>5}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-1<x<6}\\{x>5}\end{array}\right.$,
解得:5<x<6,
综上,原不等式的解集是:x<-1或5<x<6.
点评 本题考查了反比例函数与一次函数的交点问题,求不等式组的解集,正确的理解题意是解题的关键


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
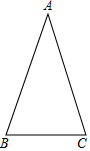 已知等腰△ABC的顶角∠A=36°(如图).
已知等腰△ABC的顶角∠A=36°(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
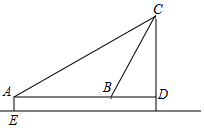 衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
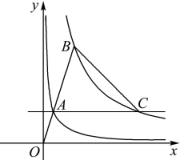 如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.
如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
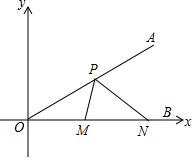 如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com