
【题目】五子棋深受广大棋友的喜爱,其规则是:在 15 15 的正方形棋盘中,由黑方先行,轮流奕子,在任何一方向(横向、竖向或斜线 方向)上连成五子者为胜。如图 3 是两个五子棋爱好者甲和乙的 部分对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若 A 点的位置记作(8,4),若不让乙在短时间内获胜,则甲必须落子 的位置是___________.

科目:初中数学 来源: 题型:
【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣mx+n与x轴交于A、B两点,与y轴交于点C(0,﹣1).且对称轴x=1.
x2﹣mx+n与x轴交于A、B两点,与y轴交于点C(0,﹣1).且对称轴x=1.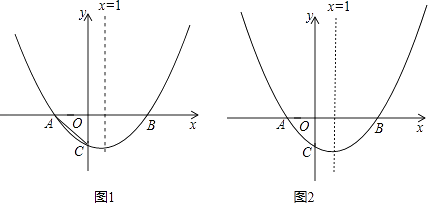
(1)求出抛物线的解析式及A、B两点的坐标;
(2)在x轴下方的抛物线上是否存在点D,使四边形ABDC的面积为3?若存在,求出点D的坐标;若不存在.说明理由(使用图1);
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,请求出所有满足条件的点P的坐标(使用图2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD=30°,AC⊥BC,AB=8cm,则△COD的面积为( )
A.![]()
cm2
B.![]()
cm2
C.![]()
cm2
D.![]()
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:点P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),….根据这个规律,求点P2018的坐标.
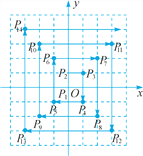
查看答案和解析>>
科目:初中数学 来源: 题型:
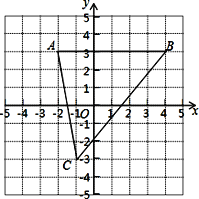
【题目】如图,已知A(-2,3)、B(4,3)、C(-1,-3)
(1)求点C到x轴的距离;
(2)求△ABC的面积;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com