
【题目】如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.
(1)分别计算获一、二、三等奖的概率.
(2)老李一次性购物满了300元,摇奖一次,获奖的概率是多少?请你预测一下老李摇奖结果会有哪几种情况?

【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,老李摇奖共有四种结果,一等奖、二等奖、三等奖、不中奖
,老李摇奖共有四种结果,一等奖、二等奖、三等奖、不中奖
【解析】
(1)找到红色区域的份数占总份数的多少即为获得一等奖的概率;找到黄色区域和蓝色区域的份数占总份数的多少即为获得二等奖、三等奖的概率.
(2)用有颜色的区域数除以所有扇形的个数即可求得获奖的概率.
解:(1)整个圆周被分成了16份,红色为1份,
∴获得一等奖的概率为:![]() ;
;
整个圆周被分成了16份,黄色为2份,
∴获得二等奖的概率为:![]() =
=![]() ;
;
整个圆周被分成了16份,蓝色为4份,
∴获得三等奖的概率为![]() =
=![]() ;
;
(2)∵共分成了16份,其中有奖的有1+2+4=7份,
∴P(获奖)=![]() ;
;
老李摇奖共有四种结果,一等奖、二等奖、三等奖、不中奖.


科目:初中数学 来源: 题型:
【题目】如图1,将长为10的线段OA绕点O旋转![]() 得到OB,点A的运动轨迹为
得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
![]() 当
当![]() ______度时,PQ有最大值,最大值为______.
______度时,PQ有最大值,最大值为______.
![]() 如图2,若P是OB中点,且
如图2,若P是OB中点,且![]() 于点P,求
于点P,求![]() 的长;
的长;
![]() 如图3,将扇形AOB沿折痕AP折叠,使点B的对应点
如图3,将扇形AOB沿折痕AP折叠,使点B的对应点![]() 恰好落在OA的延长线上,求阴影部分面积.
恰好落在OA的延长线上,求阴影部分面积.
![]() 如图4,将扇形OAB沿PQ折叠,使折叠后的弧
如图4,将扇形OAB沿PQ折叠,使折叠后的弧![]() 恰好与半径OA相切,切点为C,若
恰好与半径OA相切,切点为C,若![]() ,求点O到折痕PQ的距离.
,求点O到折痕PQ的距离.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置,AD与y轴交于点E,若B(4,8).
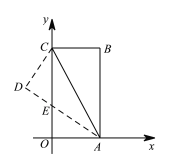
(1)△AEC是等腰三角形吗?请证明;
(2)求点D的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点P、点Q同时从点B出发,点P以
,点P、点Q同时从点B出发,点P以![]() 的速度沿
的速度沿![]() 运动,终点为C,点Q以
运动,终点为C,点Q以![]() 的速度沿
的速度沿![]() 运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,
运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,![]() 的面积为
的面积为![]() ,已知y与t的函数关系的图象如图
,已知y与t的函数关系的图象如图![]() 曲线OM和MN均为抛物线的一部分
曲线OM和MN均为抛物线的一部分![]() ,给出以下结论:
,给出以下结论:![]() ;
;![]() 曲线MN的解析式为
曲线MN的解析式为![]() ;
;![]() 线段PQ的长度的最大值为
线段PQ的长度的最大值为![]() ;
;![]() 若
若![]() 与
与![]() 相似,则
相似,则![]() 秒
秒![]() 其中正确的是
其中正确的是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年11月28日,为扩大内需,国务院决定在全国实施“家电下乡“政策.第一批列入家电下乡的产品为彩电、冰箱、洗衣机和手机四种产品.某县一家家电商场,今年一季度对以上四种产品的销售情况进行了统计,绘制了如下的统计图,根据图中信息求:

(1)彩电占四种家电下乡产品的百分比;
(2)该商场一季度冰箱销售的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=5,BC=8,若△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以点A,D,E为顶点的三角形是等腰三角形,则m的值是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com