

分析 (1)由DE∥BC,EF∥DC,可证得四边形DCFE是平行四边形,即可得EF=CD=3,CF=DE,即可得BC+DE=BF,然后利用勾股定理,求得BC+DE的值;
(2)首先连接AE,CE,由四边形ABCD是平行四边形,四边形ABEF是矩形,易证得四边形DCEF是平行四边形,继而证得△ACE是等边三角形,则可求得答案.
解答 解:(1)∵DE∥BC,EF∥DC,
∴四边形DCFE是平行四边形,
∴EF=CD=2,CF=DE,
∵CD⊥BE,
∴EF⊥BE,
∴BC+DE=BC+CF=BF=$\sqrt{B{E}^{2}+E{F}^{2}}$=$\sqrt{13}$.
(2)解决问题: 连接AE,CE,如图3.
连接AE,CE,如图3.
∵四边形ABCD是平行四边形,
∴AB∥DC.
∵四边形ABEF是矩形,
∴AB∥FE,BF=AE.
∴DC∥FE.
∴四边形DCEF是平行四边形.
∴CE∥DF.
∵AC=BF=DF,
∴AC=AE=CE.
∴△ACE是等边三角形.
∴∠ACE=60°.
∵CE∥DF,
∴∠DGC=∠ACE=60°.
点评 此题考查了平行四边形的判定与性质、矩形的性质、等边三角形的判定与性质以及勾股定理.注意掌握辅助线的作法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
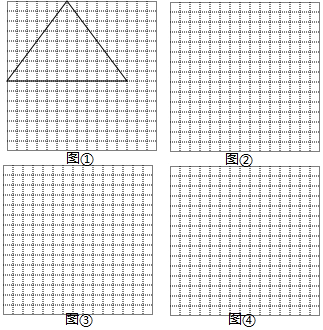 如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.
如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
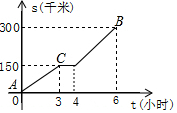 杨师傅开车从A地出发去300千米远的B地游玩,其行驶路程s与时间t之间的关系如图所示,出发一段时间后,汽车发生故障,需停车检修,修好后又继续行驶.根据题意回答下列问题:
杨师傅开车从A地出发去300千米远的B地游玩,其行驶路程s与时间t之间的关系如图所示,出发一段时间后,汽车发生故障,需停车检修,修好后又继续行驶.根据题意回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
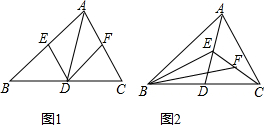 (1)如图1,已知△ABC,点D,E,F分别是BC,AB,AC的中点,若△ABC的面积为16,则△ABD的面积是8,△EBD的面积是4.
(1)如图1,已知△ABC,点D,E,F分别是BC,AB,AC的中点,若△ABC的面积为16,则△ABD的面积是8,△EBD的面积是4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com