
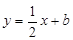 与
与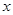 轴交于点A(-4,0),与
轴交于点A(-4,0),与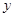 轴交于点B.
轴交于点B.
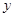 轴的
轴的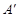 处,点B若在
处,点B若在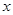 轴的
轴的 处;
处;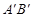 的函数关系式;
的函数关系式;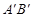 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△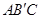 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段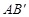 上,点M在线段
上,点M在线段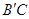 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长. 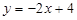 ,8或6解析:
,8或6解析: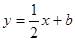 ,得
,得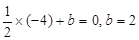
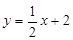 ,令
,令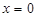 ,得
,得 ,∴B(0,2)
,∴B(0,2) 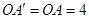 ,
, 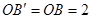
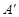 (0,4),
(0,4),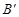 (2,0)
(2,0) 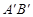 的解析式为
的解析式为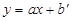
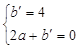 解得
解得 ∴直线
∴直线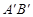 的解析式为
的解析式为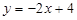
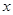 ,
,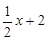 ) (
) (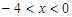 )
)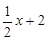
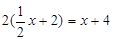
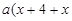 ,0), M(
,0), M(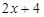 ,
,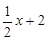 )
)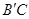 上, ∴
上, ∴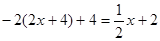
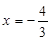 , 此时
, 此时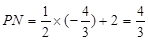 ,PQ=
,PQ=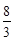
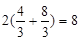
 PN=
PN=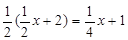
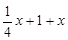 ,0), M(
,0), M(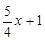 ,
,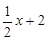 )
)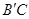 上,∴
上,∴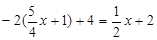
 ,此时PN=2,PQ=1
,此时PN=2,PQ=1

科目:初中数学 来源: 题型:
已知直线![]() 与
与![]() 轴交于点A(-4,0),与
轴交于点A(-4,0),与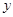 轴交于点B.
轴交于点B.

1.求b的值
2.把△AOB绕原点O顺时针旋转90°后,点A落在![]() 轴的
轴的![]() 处,点B若在
处,点B若在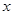 轴的
轴的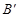 处;
处;
①求直线![]() 的函数关系式;
的函数关系式;
②设直线AB与直线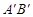 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△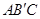 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段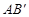 上,点M在线段
上,点M在线段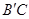 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
查看答案和解析>>
科目:初中数学 来源:2012届上海市杨浦初三基础测试数学试卷(带解析) 题型:解答题
已知直线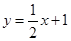 与
与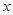 轴交于点
轴交于点 ,与
,与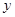 轴交于点
轴交于点 ,将三角形
,将三角形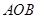 绕点
绕点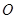 顺时针旋转90°,使点
顺时针旋转90°,使点 落在点
落在点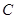 ,点
,点 落在点
落在点 ,抛物线
,抛物线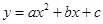 过点
过点 、
、 、
、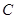 ,其对称轴与直线
,其对称轴与直线 交于点
交于点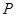 .
.
(1)求抛物线的表达式;
(2)求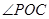 的正切值;
的正切值;
(3)点 在
在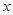 轴上,且△
轴上,且△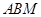 与△
与△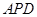 相似,求点
相似,求点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市杨浦初三基础测试数学试卷(解析版) 题型:解答题
已知直线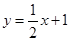 与
与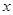 轴交于点
轴交于点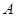 ,与
,与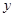 轴交于点
轴交于点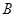 ,将三角形
,将三角形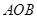 绕点
绕点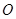 顺时针旋转90°,使点
顺时针旋转90°,使点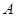 落在点
落在点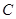 ,点
,点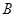 落在点
落在点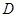 ,抛物线
,抛物线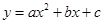 过点
过点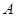 、
、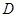 、
、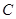 ,其对称轴与直线
,其对称轴与直线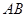 交于点
交于点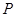 .
.
(1)求抛物线的表达式;
(2)求 的正切值;
的正切值;
(3)点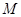 在
在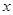 轴上,且△
轴上,且△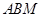 与△
与△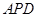 相似,求点
相似,求点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:2013届福建省泉州市八年级期中考数学试卷(解析版) 题型:解答题
已知直线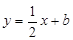 与
与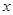 轴交于点A(-4,0),与
轴交于点A(-4,0),与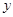 轴交于点B.
轴交于点B.

1.求b的值
2.把△AOB绕原点O顺时针旋转90°后,点A落在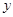 轴的
轴的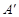 处,点B若在
处,点B若在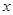 轴的
轴的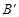 处;
处;
①求直线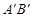 的函数关系式;
的函数关系式;
②设直线AB与直线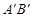 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△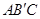 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段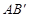 上,点M在线段
上,点M在线段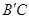 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com