
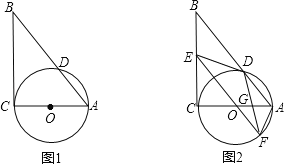
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D.
(1)在图(1)中,用直尺和圆规过点D作⊙O的切线DE交BC于点E;(保留作图痕迹,不写作法)
(2)如图(2),如果⊙O的半径为3,ED=4,延长EO交⊙O于F,连接DF,与OA交于点G,求OG的长.
【答案】(1)见解析;(2)OG=![]() .
.
【解析】
(1)连接OD,作∠COD的平分线交BC于点E,连接DE,DE就是⊙O的切线;
(2)连接OD,CD.CD与FF交于点H,根据切线长定理可得OE⊥CD, 然后利用勾股定理可得AD=![]() .由题意易得OE∥AB,于是易证△OFG∽△ADG,根据相似三角形对应线段成比例,即可求出OG的长.
.由题意易得OE∥AB,于是易证△OFG∽△ADG,根据相似三角形对应线段成比例,即可求出OG的长.
(1)切线DE如图所示;
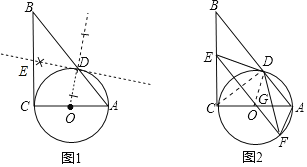
(2)连接CD,OD;
由题意EC、ED是⊙O的切线,
∴EC=ED,∵OC=OD,
∴OE⊥CD,
∵AC是直径,
∴∠CDA=90°,
∴CD⊥AB,
∴OE∥AB,
∴![]() ,
,
在Rt△ECO中,EO=![]() =5,
=5,
∵∠EOC=∠CAD,
∴cos∠CAD=cos∠EOC=![]() =
=![]() ,
,
∴AD=![]() ,设OG=x,
,设OG=x,
则有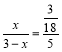 ,
,
∴x=![]() ,
,
∴OG=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
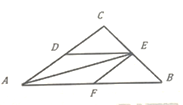
【题目】如图,在△ABC中,AB=3+![]() ,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
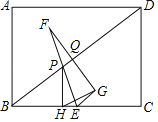
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是BC的中点,点P为对角线BD上的动点,设BP=t(t>0),作PH⊥BC于点H,连接EP并延长至点F,使得PF=PE,作点F关于BD的对称点G,FG交BD于点Q,连接GH,GE.
(1)求证:EG∥PQ;
(2)当点P运动到对角线BD中点时,求△EFG的周长;
(3)在点P的运动过程中,△GEH是否可以为等腰三角形?若可以,求出t的值;若不可以,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
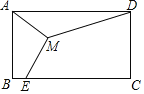
【题目】如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为( )
A. 3+2![]() B. 4+3
B. 4+3![]() C. 2+2
C. 2+2![]() D. 10
D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
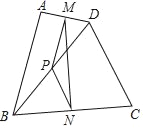
【题目】如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为( )
A. 50° B. 25° C. 15° D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
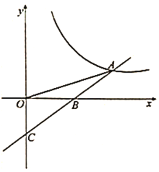
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E,F,则图中阴影部分的面积为________.
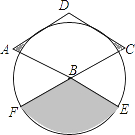
查看答案和解析>>
科目:初中数学 来源: 题型:
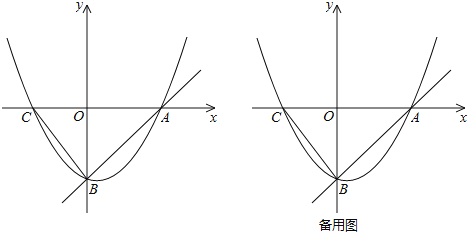
【题目】如图,直线y=x﹣4与x轴、y轴分别交于A、B两点,抛物线y=![]() x2+bx+c经过A、B两点,与x轴的另一个交点为C,连接BC.
x2+bx+c经过A、B两点,与x轴的另一个交点为C,连接BC.
(1)求抛物线的解析式及点C的坐标;
(2)点M在抛物线上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;
(3)点P从点C出发,沿线段CA由C向A运动,同时点Q从点B出发,沿线段BC由B向C运动,P、Q的运动速度都是每秒1个单位长度,当Q点到达C点时,P、Q同时停止运动,试问在坐标平面内是否存在点D,使P、Q运动过程中的某一时刻,以C、D、P、Q为顶点的四边形为菱形?若存在,直接写出点D的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com