
 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒$\frac{2π}{3}$个单位长度,则2015秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒$\frac{2π}{3}$个单位长度,则2015秒时,点P的坐标是( )| A. | (2015,0) | B. | (2015,$\sqrt{3}$) | C. | (2015,-$\sqrt{3}$) | D. | (2016,0) |
分析 设第n秒运动到Pn(n为自然数)点,根据点P的运动规律找出部分Pn点的坐标,根据坐标的变化找出变化规律“P4n+1(4n+1,$\sqrt{3}$),P4n+2(4n+2,0),P4n+3(4n+3,-$\sqrt{3}$),P4n+4(4n+4,0)”,依此规律即可得出结论.
解答 解:设第n秒运动到Pn(n为自然数)点,
观察,发现规律:P1(1,$\sqrt{3}$),P2(2,0),P3(3,-$\sqrt{3}$),P4(4,0),P5(5,$\sqrt{3}$),…,
∴P4n+1(4n+1,$\sqrt{3}$),P4n+2(4n+2,0),P4n+3(4n+3,-$\sqrt{3}$),P4n+4(4n+4,0).
∵2015=4×503+3,
∴P2015为(2015,-$\sqrt{3}$).
故选C.
点评 本题考查了规律型中的点的坐标,解题的关键是找出变化规律“P4n+1(4n+1,$\sqrt{3}$),P4n+2(4n+2,0),P4n+3(4n+3,-$\sqrt{3}$),P4n+4(4n+4,0)”.本题属于中档题,难度不大,解决该题型题目时,根据运动的规律找出点的坐标,根据坐标的变化找出坐标变化的规律是关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,直线AB与CD相交于点O.
如图,直线AB与CD相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
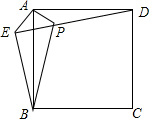 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:
已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=6600}\\{x=2y+600}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6600}\\{y=2x+600}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=6600}\\{y=2x-600}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=6600}\\{x=2y-600}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P,求证:
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com