
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
【答案】(1)60;(2)四边形ACFD是菱形.理由见解析.
【解析】试题分析:(1)、利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;
(2)、利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.
试题解析:(1)、∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC, ∴AC=DC,∠A=60°, ∴△ADC是等边三角形, ∴∠ACD=60°, ∴n的值是60;
(2)、四边形ACFD是菱形; 理由:∵∠DCE=∠ACB=90°,F是DE的中点, ∴FC=DF=FE,
∵∠CDF=∠A=60°, ∴△DFC是等边三角形, ∴DF=DC=FC, ∵△ADC是等边三角形,
∴AD=AC=DC, ∴AD=AC=FC=DF, ∴四边形ACFD是菱形.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
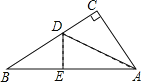
A. 3cmB. 4cmC. 5cmD. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先填写表,通过观察后再回答问题:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | x | 1 | y | 100 | …… |
(1)表格中,x=_________,y=_________
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ,则
,则![]() ≈___________
≈___________
②已知![]() ,若
,若![]() ,用含m的代数式表示b,则b=___________
,用含m的代数式表示b,则b=___________
(3)试比较![]() 与a的大小(直接写出结果)
与a的大小(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 和△BDE 都是等边三角形,A、B、D 三点共线.下列结论:①AB=CD;②BF=BG;③HB 平分∠AHD;④∠AHC=60°,⑤△BFG 是等边三角形.其中正确的有____________(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
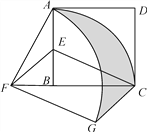
【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF、CG.
(1)求证:EF∥CG;
(2)求点C、点A在旋转过程中形成的![]() 、
、![]() 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )

A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )

A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩,根据统计图中的信息,下列结论正确的是( )
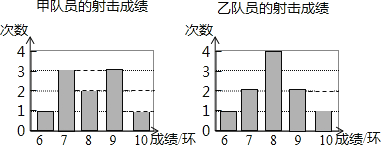
A. 甲队员成绩的平均数比乙队员的大
B. 乙队员成绩的平均数比甲队员的大
C. 甲队员成绩的中位数比乙队员的大
D. 甲队员成绩的方差比乙队员的大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com