
 有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
分析 (2)①把x=-2代入函数解析式可求得m的值;
②观察给定表格中的数据可发现函数图象上的点关于点(2,0)对称,再根据点M、N的坐标即可求出n值;
(3)①找出点A关于点(2,0)对称的点B1,再找出与点B1纵坐标相等的B2点;
②根据表格描点、连线即可得出函数图象.
解答 解:(2)①当x=-2时,y=(x-1)(x-2)(x-3)=-60.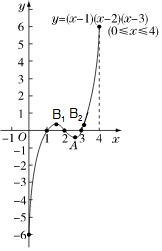
故答案为:-60.
②观察表格中的数据可得出函数图象关于点(2,0)中心对称,
∴-7+n=2×2,解得:n=11.
故答案为:11.
(3)①作点A关于点(2,0)的对称点B1,再在函数图象上找与点B1纵坐标相等的B2点.
②根据表格描点、连线,画出图形如图所示.
点评 本题考查了多次函数的图象与性质,根据给定表格找出函数图象关于点(2,0)中心对称是解题的关键.


科目:初中数学 来源: 题型:选择题
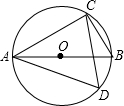 如图,已知AB是圆O的直径,∠CAB=30°,则cosD的值为( )
如图,已知AB是圆O的直径,∠CAB=30°,则cosD的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+1)2 | B. | (x-1)2 | C. | $\frac{1}{(x+1)^{2}}$ | D. | $\frac{1}{(x-1)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
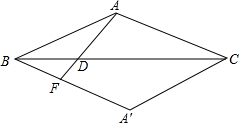 如图:等腰三角形ABC中,∠ABC=20°,将△ABC沿BC向下翻折得到△A′BC.已知D为线段BC上一点.连接AD,并延长AD交A′B于点F,若∠BAD=∠ABC,BF=3,CD=5,那么△ACD的面积为$\frac{15}{4}\sqrt{3}$.
如图:等腰三角形ABC中,∠ABC=20°,将△ABC沿BC向下翻折得到△A′BC.已知D为线段BC上一点.连接AD,并延长AD交A′B于点F,若∠BAD=∠ABC,BF=3,CD=5,那么△ACD的面积为$\frac{15}{4}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(立方米) | 收费(元) |
| 5 | 9 | 14.4 |
| 6 | 13 | 23.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是⊙O的内接四边形,P是对角线BD上的一个动点,连接OP,若⊙O的半径为1,∠A:∠C=1;2,则OP+$\frac{1}{2}$BP的最小值为$\frac{\sqrt{3}}{2}$.
如图,四边形ABCD是⊙O的内接四边形,P是对角线BD上的一个动点,连接OP,若⊙O的半径为1,∠A:∠C=1;2,则OP+$\frac{1}{2}$BP的最小值为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com