
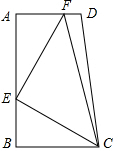
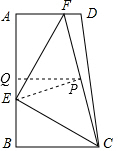
 (2013•海珠区一模)如图,在直角梯形ABCD中,∠A=∠B=90°,AD=5,AB=10,BC=6,点E是线段AB上的动点,连结CE,EF⊥CE交AD于F,连结CF,设BE=x.
(2013•海珠区一模)如图,在直角梯形ABCD中,∠A=∠B=90°,AD=5,AB=10,BC=6,点E是线段AB上的动点,连结CE,EF⊥CE交AD于F,连结CF,设BE=x.| 2 |
| AF+BC |
| 2 |
| CF |
| 2 |
| 2 |
| 2 |
| 3 |
| BC |
| cos300 |
| 3 |
| 3 |
| AF+BC |
| 2 |
| CF |
| 2 |
| AF+BC |
| 2 |
| CF |
| 2 |
| AF+BC |
| 2 |
| CF |
| 2 |
| 2 |
| 2 |
| EB |
| FA |
| BC |
| AE |
| x |
| 2|5-x|-6 |
| 6 |
| 10-x |
| x |
| 4-2x |
| 6 |
| 10-x |
| 97 |
| 97 |
| x |
| 2x-16 |
| 6 |
| 10-x |
| 97 |
| 97 |
| 97 |
| 97 |
| 2 |


科目:初中数学 来源: 题型:
(2013•海珠区一模)一次数学测验,甲、乙两班的数学成绩统计数据如表:
(1)从平均分来看,甲、乙两班学生的数学成绩平均水平相同; (2)如果不低于120分为优秀,那么甲班获得优秀的人数比乙班多; (3)甲班同学的成绩波动相对比较大. 上述结论正确的是( ) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com