
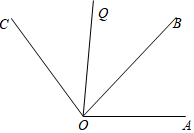
 ��ͼ��OQ�ǡ�BOC��ƽ���ߣ�
��ͼ��OQ�ǡ�BOC��ƽ���ߣ����� ��1�����ݽ�ƽ���ߵij߹���ͼ���ɵã�
��2����OPƽ�֡�AOB֪$��POB=\frac{1}{2}$��AOB����OQƽ�֡�BOC֪��BOQ=$\frac{1}{2}$��BOC�����ݡ�POQ=��POB+��BOQ�ɵô𰸣�
��� �⣺��1����ͼ��OP��Ϊ����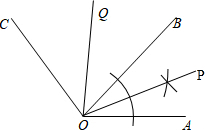
��2����POQ���AOC֮���������ϵ�ǣ���POQ=$\frac{1}{2}��AOC$��
��ΪOP�ǡ�AOB��ƽ���ߣ�
����$��POB=\frac{1}{2}$��AOB��
ͬ����$��BOQ=\frac{1}{2}$��BOC��
���ǡ�POQ=��POB+��BOQ=$\frac{1}{2}$��AOB$+\frac{1}{2}$��BOC=$\frac{1}{2}$����AOB+��BOC��=$\frac{1}{2}$��AOC��
�ʴ�Ϊ����POB����BOQ����AOB����BOC����AOB����BOC����AOC��
���� ������Ҫ������ͼ-�߹���ͼ����ƽ���ߵĶ��壬����Ĺؼ����������ս�ƽ���ߵij߹���ͼ����ƽ���ߵĶ�������ʣ�


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ڡ�ABC�У�AB=6��AC=4��D���߶�AB�ϵ�һ�㣬��AD=2����E���߶�AC�ϵ�һ�㣬�ҡ�ADE���ABC���ƣ���AE=$\frac{4}{3}$��3��
�ڡ�ABC�У�AB=6��AC=4��D���߶�AB�ϵ�һ�㣬��AD=2����E���߶�AC�ϵ�һ�㣬�ҡ�ADE���ABC���ƣ���AE=$\frac{4}{3}$��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
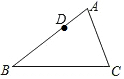
 ��ͼ��C���߶�AB������һ�㣬D��E�ֱ����߶�BC��AC���е㣬��AB=14����DE�ij�Ϊ7��
��ͼ��C���߶�AB������һ�㣬D��E�ֱ����߶�BC��AC���е㣬��AB=14����DE�ij�Ϊ7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ⲻ��ʽ�飺$\left\{\begin{array}{l}{x-3��0����}\\{\frac{3x+1}{12}��\frac{2x-1}{3}����}\end{array}\right.$���Ѳ���ʽ��Ľ⼯��ʾ�������ϣ�
�ⲻ��ʽ�飺$\left\{\begin{array}{l}{x-3��0����}\\{\frac{3x+1}{12}��\frac{2x-1}{3}����}\end{array}\right.$���Ѳ���ʽ��Ľ⼯��ʾ�������ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
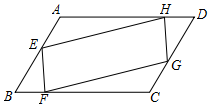 ��֪����ͼ��ƽ���ı���ABCD��E��F��G��H�ֱ���AB��BC��CD��AD�ϵĵ㣬��AE=CG��BF=DH��
��֪����ͼ��ƽ���ı���ABCD��E��F��G��H�ֱ���AB��BC��CD��AD�ϵĵ㣬��AE=CG��BF=DH���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
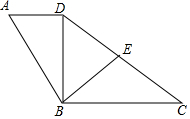 ��֪����ͼ�����ı���ABCD�У�AB=3��BC=4��AD��BC����ADB=90�㣬cosA=$\frac{1}{3}$��
��֪����ͼ�����ı���ABCD�У�AB=3��BC=4��AD��BC����ADB=90�㣬cosA=$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x-��y+z��=x+y-z | B�� | -��x-y-z��=-x+y-z | ||
| C�� | a-2��b+c��=a-2b-c | D�� | -��a-b��-2��-c��=-a+b+2c |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com