
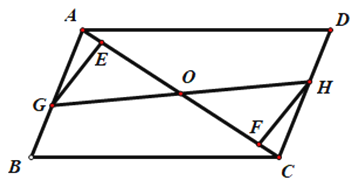
【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.
【答案】(1)见解析 (2)见解析
【解析】
(1)由平行四边形的性质得到AB平行CD,得到内错角∠GAO=∠FCH,根据AF=CE,同时减去EF可得AE=CF,根据SAS可证△ AGE≌△CHF,得到∠AEG=∠CFH,再由邻补角得到内错角相等,得到两线平行;
(2)连接FG、EH ,由(1)可证四边形EGFH是平行四边形即可得到结论.
在ABCD中,
∵AB∥CD,
∴∠GAE=∠HCF,
∵AF=CE,
∴AF-EF=CE=EF,
即;AE=CF,
在△AGE与△CHF中,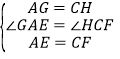 ,
,
∴△AGE≌△CHF(SAS),
∴∠AEG=∠CFH,
∴∠GEO=∠HFO,
∴EG∥FH;
(2)连接FG、EH
由(1)证得△AGE≌△CHF ,EG∥FH,
∴GE=HF,
∴四边形GFHE是平行四边形,
∴GH、EF互相平分.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:
【题目】定义一种新运算“a*b”:当a≥b时,a*b=a+2b;当a<b时,a*b=a-2b.
例如:3*(-4)=3+(-8)=-5,(-6)*12=-6-24=-30
(1)填空:(-4)*3= .
(2)若(3x-4)*(x+6)=(3x-4)+2(x+6),则x的取值范围为 ;
(3)已知(3x-7)*(3-2x)<-6,求x的取值范围;
(4)小明在计算(2x2-4x+8)*(x2+2x-2)时随意取了一个x的值进行计算,得出结果是-4,小丽告诉小明计算错了,问小丽是如何判断的.
查看答案和解析>>
科目:初中数学 来源: 题型:
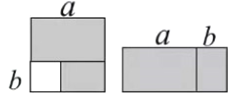
【题目】如图,从边长为![]() 的正方形内去掉一个边长为
的正方形内去掉一个边长为![]() 的小正方形,然后将剩余部分拼成一个长方形。
的小正方形,然后将剩余部分拼成一个长方形。
(1)上述操作所能验证的公式是 ;
(2)求大正方形和拼成的长方形的周长;
(3)用一根长为![]() 的铁丝围成一个长方形,什么情况下围成的面积最大,最大面积为多少?
的铁丝围成一个长方形,什么情况下围成的面积最大,最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乒乓球的质量检验结果如下:
抽取的乒乓球数n | 50 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
优等品的频数m | 48 | 95 | 188 | x | 948 | 1426 | 1898 |
优等品的频率 | 0.960 | y | 0.940 | 0.944 | z | 0.951 | 0.949 |
(1)根据表中信息可得:x=______,y=______,z=______;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是多少?(精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
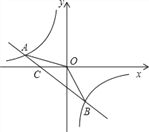
【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
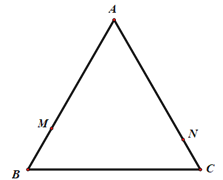
【题目】如图,等边△ABC的边长为8,动点M从点B出发,沿B→A→C→B的方向以每秒3个单位长度的速度运动,动点N从点C出发,沿C→A→B-C的方向以每秒2个单位长度的速度运动.
(1)若动点M、N同时出发,经过几秒第一次相遇?
(2)若动点M、N同时出发,且其中一点到达终点时,另一点即停止运动.在△ABC的边上是否存在一点D,使得以点A、M、N、D为顶点的四边形为平行四边形?若存在,求此时运动的时间![]() 及点D的具体位置;若不存在,请说明理由.
及点D的具体位置;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点列达终点时,另一点也停止运动,设运动的时间为t秒.
(1)求线段DO的长;
(2)设运动过程中△POQ两直角边的和为y,请求出y关于x的函数解析式;
(3)请直接写出点P在线段OC上,点Q在线段DO上运动时,△POQ面积的最大值,并写出此时的t值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com