
【题目】2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
【答案】(1)甲工程队单独完成这项工程需要20天,乙工程队单独完成这项工程需30天;(2)应选甲工程队单独完成;理由见解析.
【解析】
(1)设甲工程队单独完成这项工程需要x天,则乙工程队单独完成这项工程需要1.5x天,根据甲工程队完成的工作量+乙工程队完成的工作量=整项工程,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设甲工程队每天的费用是y元,则乙工程队每天的费用是(y﹣250)元,根据甲、乙两工程队合作12天共需费用27720元,即可得出关于y的一元一次方程,解之即可得出两队每天所需费用,再求出两队单独完成这些工程所需总费用,比较后即可得出结论.
解:(1)设甲工程队单独完成这项工程需要x天,则乙工程队单独完成这项工程需要1.5x天,
依题意,得:![]() 1,
1,
解得:x=20,
经检验,x=20是原分式方程的解,且符合题意,
∴1.5x=30.
答:甲工程队单独完成这项工程需要20天,乙工程队单独完成这项工程需30天;
(2)设甲工程队每天的费用是y元,则乙工程队每天的费用是(y﹣250)元,
依题意,得:12y+12(y﹣250)=27720,
解得:y=1280,
∴y﹣250=1030.
甲工程队单独完成共需要费用:1280×20=25600(元),
乙工程队单独完成共需要费用:1030×30=30900(元).
∵25600<30900,
∴甲工程队单独完成需要的费用低,应选甲工程队单独完成.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 在
在![]() 的边
的边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径的圆与
为半径的圆与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,并且与边
,并且与边![]() 相切于点
相切于点![]() ,连接
,连接![]() .已知
.已知![]() 平分
平分![]() .
.
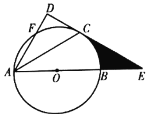
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 的半径为3.求阴影部分的面积.(结果保留
的半径为3.求阴影部分的面积.(结果保留![]() 和根号)
和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图①,若AB=1,DG=2,求BH的长;
(2)如图②,连接AH、GH,求证:AH=GH且AH⊥GH.
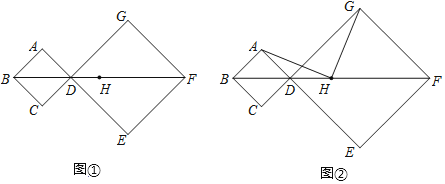
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线CP绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB重合,就停止旋转.在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.
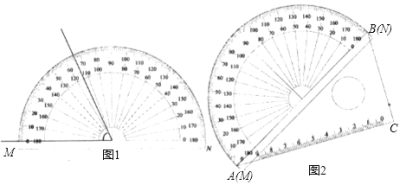
(1)设旋转x秒后,点E处的读数为y°,则y与x的函数关系式________.
(2)当CP旋转________秒时,△BCE是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y![]() (k>0,x>0)的图象经过AC的中点D,则k的值为( )
(k>0,x>0)的图象经过AC的中点D,则k的值为( )

A.4B.5C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y![]() (k>0,x>0)的图象经过AC的中点D,则k的值为( )
(k>0,x>0)的图象经过AC的中点D,则k的值为( )
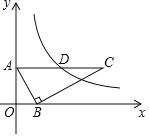
A.4B.5C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量观光塔高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,请根据以上观测数据求观光塔的高.
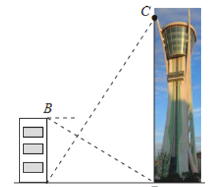
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:方程有两个不相等的实数根;
(2)设x1,x2为方程的两个实数根,且x1+2x2=14,试求出方程的两个实数根和k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
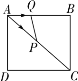
【题目】如图,已知在矩形 ABCD 中,AB=4,AD=3,连接 AC,动点 Q 以每秒 1 个单位的速度沿 A→B→C 向点 C 匀速运动,同时点 P 以每秒 2 个单位的速度沿 A→C→D 向点 D 匀速运动,连接 PQ,当点 P 到达终点 D 时,停止运 动,设△APQ 的面积为 S,运动时间为 t 秒,则 S 与 t 函数关系的图象大致为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com