练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．如果（a-b）（b-c）（c-a）=1，x、y为任意有理数．那么（b-a）（x-c）（y-c）+（c-b）（x-a）（y-a）+（a-c）（x-b）（y-b）的值为1．

    分析 将原式变形为（b-a）（x-c）（y-c）+[（c-a）+（a-b）]（x-a）（y-a）+（a-c）（x-b）（y-b），再提取公因式化简得到原式=（a-b）（b-c）（c-a），再将（a-b）（b-c）（c-a）=1代入计算即可求解．

    解答 解：（b-a）（x-c）（y-c）+（c-b）（x-a）（y-a）+（a-c）（x-b）（y-b）
    =（b-a）（x-c）（y-c）+[（c-a）+（a-b）]（x-a）（y-a）+（a-c）（x-b）（y-b）
    =（a-b）[（x-a）（y-a）-（x-c）（y-c）]+（c-a）[（x-a）（y-a）-（x-b）（y-b）]
    =（a-b）[xy-ay-ax+a2-（xy-cy-cx-c2）]+（c-a）[xy-ay-ax+a2-（xy-by-bx+b2）]
    =（a-b）[（c-a）y+（c-a）x-（c-a）（c+a）]+（c-a）[（b-a）y+（b-a）x-（b-a）（b+a）]
    =（a-b）（c-a）[（y+x）-（c+a）]+（c-a）（b-a）[（y+x）-（b+a）]
    =（a-b）（c-a）[（y+x）-（c+a）]-（y+x）+（b+a）]
    =（a-b）（c-a）（b-c）
    =（a-b）（b-c）（c-a）
    =1．
    故答案为：1．

    点评 本题考查了整式的混合运算和求值，能正确根据整式的运算法则进行化简是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．（1）计算：$\sqrt{12}$+|-5|-（$\frac{1}{4}$）-1+3tan60°；　
    （2）已知a2-2a-2=0，求代数式$\frac{1}{a-1}$-$\frac{1}{{a}^{2}-1}$÷$\frac{a-1}{{a}^{2}+2a+1}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图1，在△ABC中，设∠A、∠B、∠C的对边分别为a，b，c，过点A作AD⊥BC，垂足为D，会有sin∠C=$\frac{AD}{AC}$，则
    S△ABC=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×BC×ACsin∠C=$\frac{1}{2}$absin∠C，
    即S△ABC=$\frac{1}{2}$absin∠C
    同理S△ABC=$\frac{1}{2}$bcsin∠A
    S△ABC=$\frac{1}{2}$acsin∠B
    通过推理还可以得到另一个表达三角形边角关系的定理-余弦定理：
    如图2，在△ABC中，若∠A、∠B、∠C的对边分别为a，b，c，则
    a2=b2+c2-2bccos∠A
    b2=a2+c2-2accos∠B
    c2=a2+b2-2abcos∠C
    用上面的三角形面积公式和余弦定理解决问题：
    （1）如图3，在△DEF中，∠F=60°，∠D、∠E的对边分别是3和8．求S△DEF和DE2．
    解：S△DEF=$\frac{1}{2}$EF×DFsin∠F=6$\sqrt{3}$；
    DE2=EF2+DF2-2EF×DFcos∠F=49．
    （2）如图4，在△ABC中，已知AC＞BC，∠C=60°，△ABC'、△BCA'、△ACB'分别是以AB、BC、AC为边长的等边三角形，设△ABC、△ABC'、△BCA'、△ACB'的面积分别为S1、S2、S3、S4，求证：S1+S2=S3+S4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图是一次函数y=kx+b-1（k≠0，b是常数）的图象，则b的取值范围是（　　）
    A．b＞-1B．b＞1C．b＜1D．b＜-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

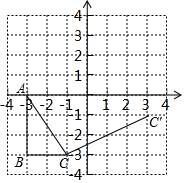    4．如图，在平面直角坐标系中，Rt△ABC的三个顶点坐标为A（-3，0），B（-3，-3），C（-1，-3）
    （1）在图中作出△ABC关于x轴对称的图形△DEF；
    （2）按要求画图，将△ABC沿CC′方向平移，使得点C移动至图中点C′的位置．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，一次函数y=k1x+5（k1＜0）的图象与坐标轴交于A，B两点，与反比例函数y=$\frac{{k}_{2}}{x}$（k2＞0）的图象交于M，N两点，过点M作MC⊥y轴于点C，已知CM=1．
    （1）求k2-k1的值；
    （2）若$\frac{AM}{AN}$=$\frac{1}{4}$，求反比例函数的解析式；
    （3）在（2）的条件下，设点P是x轴（除原点O外）上一点，将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ，当点P滑动时，点Q能否在反比例函数的图象上？如果能，求出所有的点Q的坐标；如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列调查中，最适合采用普查方式的是（　　）
    A．调查江北中小学的睡眠时间
    B．调查重庆市初中生的兴趣爱好
    C．调查中国中学教师的健康状况
    D．调查“天宫二号”飞行器各零部件质量

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．某跳远运动员备战里约2016夏季奥运会，对自己的训练效果进行测试，6次跳远成绩的平均数为7.8m，方差为$\frac{1}{60}$，如果他再跳两次，成绩分别为7.6m，8.0m，则该运动员这8次跳远成绩的方差将（　　）
    A．变大B．变小C．不变D．不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．在△ABC中．∠A=50°．AB，AC边上的高所在直线交于点H．则∠BHC的度数是140°或50°．

    查看答案和解析>>

    同步练习册答案