
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点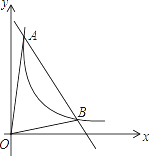
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b< ![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
【答案】
(1)解:∵点A(m,6),B(3,n)两点在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1,n=2, 即A(1,6),B(3,2). 又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴ ![]() . 解得
. 解得 ![]() ,
,
则该一次函数的解析式为:y=﹣2x+3
(2)解:根据图象可知使kx+b< ![]() 成立的x的取值范围是0<x<1或x>2;
成立的x的取值范围是0<x<1或x>2;
(3)解:分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2), 则 ![]() =4×6÷2-4×2÷2=12-4=8
=4×6÷2-4×2÷2=12-4=8
【解析】 (1)先将点A、B的坐标分别代入反比例函数解析式求出这两点坐标,再利用待定系数法,求出一次函数的解析式。
(2)要求一次函数值小于反比例函数值,要看直线x=1,直线x=3,两条直线将两函数分成三部分,这三部分的自变量的取值范围分别是0<x<1、x>3.1<<3,即可观察一次函数图象在反比例函数图象下方时所对应的x的取值范围。
(3)添加辅助线,分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点。先求出点D的坐标,然后根据![]() ,即可求出结果。或过点A作AE⊥x轴,交OB于点H,△OAB的面积=△OAH的面积+△HAB的面积.
,即可求出结果。或过点A作AE⊥x轴,交OB于点H,△OAB的面积=△OAH的面积+△HAB的面积.
【考点精析】掌握确定一次函数的表达式和反比例函数的性质是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中, ![]() 三个顶点坐标分别为
三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ;
;
(2)将![]() 的三个顶点的横坐标与纵坐标同时乘
的三个顶点的横坐标与纵坐标同时乘![]() ,得到对应的点
,得到对应的点![]() 、
、![]() 、
、![]() ,请画出
,请画出![]()
![]() ;
;
(3)求![]() 与
与![]() 的面积比,即
的面积比,即![]() :
:![]() =________(不写解答过程,直接写出结果).
=________(不写解答过程,直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,三个内角的平分线交于点
中,三个内角的平分线交于点![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .
.
(1)如图,若∠ABC=40°,则∠AOC= ,∠ADO= ;
(2)猜想![]() 与
与![]() 的关系,并说明你的理由;
的关系,并说明你的理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).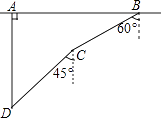
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有A、B、C三地依次在一条笔直的公路上,A、B两地相距40km,一辆甲车以40km/h的速度从B地到C地;同时一辆乙车以80km/h的速度从B地开往A地,到达A地后,然后以120km/h的速度开往C地,两车在各段内均匀速行驶,图中线段EF与折线EMN分别表示甲、乙两车距C地的路程y(千米)与行驶时间x(小时)之间的函数关系图象.
(1)写出点M的坐标为_______;点E的纵坐标的意义是________.
(2)请直接写出n,b的值,并求出线段EF与MN的函数关系式;
(3)两车出发几小时后,乙车追上甲车?
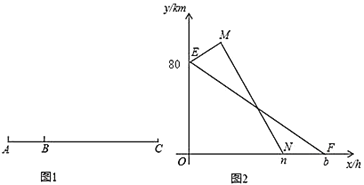
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.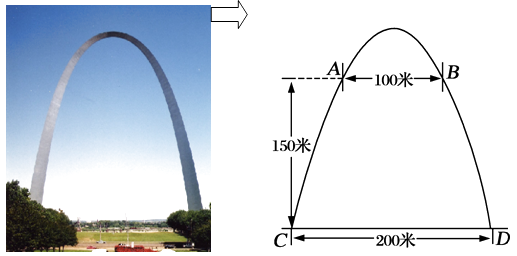
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )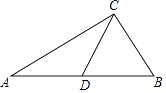
A.![]()
B.2
C.4 ![]() ﹣4
﹣4
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com