
ЁОЬтФПЁПВйзїЬНОП
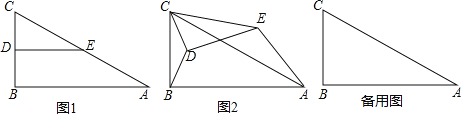
ШчЭМ1ЃЌдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌABЃН4ЃЌBCЃН2ЃЌЕуDЁЂEЗжБ№ЪЧБпBCЁЂACЕФжаЕуЃЌСЌНгDEЃЎНЋЁїCDEШЦЕуCФцЪБеыЗНЯђа§зЊЃЌМЧа§зЊНЧЮЊІСЃЎ
ЃЈ1ЃЉЮЪЬтЗЂЯж
ЂйЕБІСЃН0ЁуЪБЃЌ![]() ЃНЁЁ ЁЁЃЛЂкЕБІСЃН180ЁуЪБЃЌ
ЃНЁЁ ЁЁЃЛЂкЕБІСЃН180ЁуЪБЃЌ![]() ЃНЁЁ ЁЁЃЎ
ЃНЁЁ ЁЁЃЎ
ЃЈ2ЃЉЭиеЙЬНОП
ЪдХаЖЯЃКЕБ0ЁуЁмІСЃМ360ЁуЪБЃЌ![]() ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЎ
ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЎ
ЃЈ3ЃЉЮЪЬтНтОі
ЁїCDEШЦЕуCФцЪБеыа§зЊжСAЁЂBЁЂEШ§ЕудкЭЌвЛЬѕжБЯпЩЯЪБЃЌЧѓЯпЖЮBDЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЌЂк
ЃЌЂк![]() ЃЈ2ЃЉЕБ0ЁуЁмІСЃМ360ЁуЪБЃЌ
ЃЈ2ЃЉЕБ0ЁуЁмІСЃМ360ЁуЪБЃЌ![]() ЕФДѓаЁУЛгаБфЛЏЃЈ3ЃЉBDЕФГЄЮЊ
ЕФДѓаЁУЛгаБфЛЏЃЈ3ЃЉBDЕФГЄЮЊ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйЕБІСЃН0ЁуЪБЃЌдђЕуDЁЂEЗжБ№ЪЧБпBCЁЂACЕФжаЕуЃЌЕУDEЁЮBAЃЌНјЖјМДПЩЕУЕНД№АИЃЛЂкЕБІСЃН180ЁуЪБЃЌдђЕуDЁЂEЗжБ№ЪЧБпBCЁЂACЕФбгГЄЯпЩЯЃЌЧвDEЁЮBAЃЌгЩ![]() ЃЌМДПЩЕУЕНД№АИЃЛ
ЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉИљОнСНБпЖдгІГЩБШР§ЧвМаНЧЯрЕШЕФСНИіШ§НЧаЮЯрЫЦЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃКЂйЕБЕуEдкABЕФбгГЄЯпЩЯЪБЃЌ ЂкЕБЕуEдкЯпЖЮABЩЯЪБЃЌ НсКЯ![]() ЃН
ЃН![]() ЃЌЗжБ№ЧѓГіД№АИЃЌМДПЩЃЎ
ЃЌЗжБ№ЧѓГіД№АИЃЌМДПЩЃЎ
ЃЈ1ЃЉЂйЁпдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌABЃН4ЃЌBCЃН2ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБІСЃН0ЁуЪБЃЌдђЕуDЁЂEЗжБ№ЪЧБпBCЁЂACЕФжаЕуЃЌ
ЁрDEЁЮBAЃЌ
Ёр![]() ЃЌМДЃК
ЃЌМДЃК![]() ЃЌ
ЃЌ
ЙЪД№АИЪЧЃК![]() ЃЛ
ЃЛ
ЂкЕБІСЃН180ЁуЪБЃЌдђЕуDЁЂEЗжБ№ЪЧБпBCЁЂACЕФбгГЄЯпЩЯЃЌЧвDEЁЮBAЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
Ёр ![]() ЃЎ
ЃЎ
ЙЪД№АИЪЧЃК![]() ЃЛ
ЃЛ
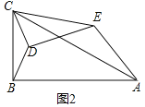
ЃЈ2ЃЉШчЭМ2ЃЌЕБ0ЁуЁмІСЃМ360ЁуЪБЃЌ![]() ЕФДѓаЁУЛгаБфЛЏЃЌРэгЩШчЯТЃК
ЕФДѓаЁУЛгаБфЛЏЃЌРэгЩШчЯТЃК
ЁпЁЯECDЃНЁЯACBЃЌ
ЁрЁЯECAЃНЁЯDCBЃЌ
ЁпЕуDЁЂEЗжБ№ЪЧБпBCЁЂACЕФжаЕуЃЌМДЃКCD=1ЃЌCE=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЁрЁїECAЁзЁїDCBЃЌ
Ёр![]() =
=![]() =
=![]() ЃЛ
ЃЛ
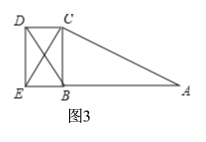
ЃЈ3ЃЉЂйЕБЕуEдкABЕФбгГЄЯпЩЯЪБЃЌШчЭМ3ЃЌ
дкRtЁїBCEжаЃЌCEЃН![]() ЃЌBCЃН2ЃЌ
ЃЌBCЃН2ЃЌ
ЁрBEЃН![]() ЃН
ЃН![]() ЃН1ЃЌ
ЃН1ЃЌ
ЁрAEЃНAB+BEЃН5ЃЌ
Ёп![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрBDЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
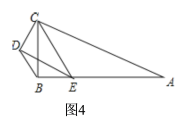
ЂкЕБЕуEдкЯпЖЮABЩЯЪБЃЌШчЭМ4ЃЌ
ЁпBC=2ЃЌCE=![]() ЃЌЁЯABC=90ЁуЃЌ
ЃЌЁЯABC=90ЁуЃЌ
ЁрBEЃН1ЃЌAEЃН4Љ1ЃН3ЃЌ
Ёп![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрBDЃН![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФBDЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгывЛДЮКЏЪ§
ЕФЭМЯѓгывЛДЮКЏЪ§![]() ЕФЭМЯѓНЛгкЕу
ЕФЭМЯѓНЛгкЕу![]() МАЕу
МАЕу![]()
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНМА![]() ЕФзјБъ
ЕФзјБъ
ЃЈ2ЃЉИљОнЭМЯѓЃЌжБАДаДГіТњзу![]() ЕФ
ЕФ![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаЯњЪлвЛжжЪщАќЃЌЦНОљУПЬьПЩЯњЪл100МўЃЌУПМўгЏРћ30дЊ.ЪдгЊЯњНзЖЮЗЂЯжЃКИУЩЬЦЗУПМўНЕМл1дЊЃЌГЌЪаЦНОљУПЬьПЩЖрЪлГі10Мў.ЩшУПМўЩЬЦЗНЕМл![]() дЊЪБЃЌШегЏРћЮЊ
дЊЪБЃЌШегЏРћЮЊ![]() дЊ.ОнДЫЙцТЩЃЌНтОіЯТСаЮЪЬтЃК
дЊ.ОнДЫЙцТЩЃЌНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉНЕМлКѓУПМўЩЬЦЗгЏРћ дЊЃЌГЌЪаШеЯњЪлСПдіМг МўЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉдкЩЯЪіЬѕМўВЛБфЕФЧщПіЯТЃЌЧѓУПМўЩЬЦЗНЕМлЖрЩйдЊЪБЃЌГЌЪаЕФШегЏРћзюДѓЃПзюДѓЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
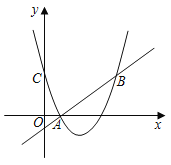
ЁОЬтФПЁПШчЭМ1,вбжЊжБЯпyЃНaгыХзЮяЯп![]() НЛгкAЁЂBСНЕу(AдкBЕФзѓВр),НЛyжсгкЕуC
НЛгкAЁЂBСНЕу(AдкBЕФзѓВр),НЛyжсгкЕуC
(1)ШєABЃН4,ЧѓaЕФжЕ
(2)ШєХзЮяЯпЩЯДцдкЕуD(ВЛгыAЁЂBжиКЯ),ЪЙ![]() ,ЧѓaЕФШЁжЕЗЖЮЇ
,ЧѓaЕФШЁжЕЗЖЮЇ
(3)ШчЭМ2,жБЯпyЃНkxЃЋ2гыХзЮяЯпНЛгкЕуEЁЂF,ЕуPЪЧХзЮяЯпЩЯЕФЖЏЕу,бгГЄPEЁЂPFЗжБ№НЛжБЯпyЃНЃ2гкMЁЂNСНЕу,MNНЛyжсгкQЕу,ЧѓQMЁЄQNЕФжЕЁЃ
ЭМ1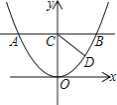 ЭМ2
ЭМ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮADЕФБпГЄЮЊ2ЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌBD=2ЃЌЗжБ№вдABЁЂBCЮЊжБОЖзїАыдВЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДЋЫЕЙХЯЃРАБЯДяИчРЫЙбЇХЩЕФЪ§бЇМвОГЃдкЩГЬВЩЯбаОПЪ§бЇЮЪЬтЃЌЫћУЧдкЩГЬВЩЯЛЕуЛђгУаЁЪЏзгРДБэЪОЪ§ЃЌБШШчЃЌЫћУЧбаОПЙ§1,3,6,10ЃЌЁЁЃЌгЩгкетаЉЪ§ПЩвдгУЭМжаЫљЪОЕФШ§НЧаЮЕуеѓБъБэЪОЃЌЫћУЧОЭНЋЦфГЦЮЊШ§НЧаЮЪ§ЃЌЕкnИіШ§НЧаЮЪ§ПЩвдгУ![]() БэЪО.
БэЪО.
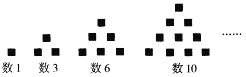
ЧыИљОнвдЩЯВФСЯЃЌжЄУївдЯТНсТлЃК
(1)ШЮвтвЛИіШ§НЧаЮЪ§ГЫ8дйМг1ЪЧвЛИіЭъШЋЦНЗНЪ§ЃЛ
(2)СЌајСНИіШ§НЧаЮЪ§ЕФКЭЪЧвЛИіЭъШЋЦНЗНЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаТЛЊЩЬГЁЯњЪлФГжжБљЯфЃЌУПЬЈНјМлЮЊ2500дЊЃЌЯњЪлМлЮЊ2900дЊЃЌЦНОљУПЬьФмЪлГі8ЬЈЃЛЕїВщЗЂЯжЃЌЕБЯњЪлМлУПНЕЕЭ50дЊЃЌЦНОљУПЬьОЭФмЖрЪлГі4ЬЈЃЎЩЬГЁвЊЯыЪЙетжжБљЯфЕФЯњЪлРћШѓЦНОљУПЬьДяЕН5000дЊЃЌУПЬЈБљЯфгІИУНЕМлЖрЩйдЊЃПШєЩшУПЬЈБљЯфНЕМлxдЊЃЌИљОнЬтвтПЩСаЗНГЬЃЈЁЁЁЁЃЉ
A. (2900-x)(8+4ЁС![]() )=5000 B. (400-x)(8+4ЁС
)=5000 B. (400-x)(8+4ЁС![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2ЉЃЈ2k+1ЃЉx+k2+1ЃН0ЃЎ
ЃЈ1ЃЉШєЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєЗНГЬЕФСНИљЧЁКУЪЧвЛИіОиаЮСНСкБпЕФГЄЃЌЧвkЃН2ЃЌЧѓИУОиаЮЕФЖдНЧЯпLЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГВЉЮяЙнУПжмЖМЮќв§ДѓСПжаЭтгЮПЭЧАРДВЮЙлЃЌШчЙћгЮПЭЙ§ЖрЃЌЖдЙнжаЕФефЙѓЮФЮяЛсВњЩњВЛРћгАЯьЃЌЕЋЭЌЪБПМТЧЕНЮФЮяЕФаоЩЩКЭБЃДцЗбгУЮЪЬтЃЌЛЙвЊБЃжЄвЛЖЈЕФУХЦБЪеШыЃЌвђДЫЃЌВЉЮяЙнВЩШЁСЫеЧИЁУХЦБМлИёЕФЗНЗЈРДПижЦВЮЙлШЫЪ§ЃЌдкИУЗНЗЈЪЕЪЉЙ§ГЬжаЗЂЯжЃКУПжмВЮЙлШЫЪ§гыЦБМлжЎМфДцдкзХШчЭМЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕЃЎдкетжжЧщПіЯТЃЌШчЙћвЊБЃжЄУПжм![]() ЭђдЊЕФУХЦБЪеШыЃЌФЧУДУПжмгІЯоЖЈВЮЙлШЫЪ§ЪЧЖрЩйЃПУХЦБМлИёгІЪЧЖрЩйЃЎ
ЭђдЊЕФУХЦБЪеШыЃЌФЧУДУПжмгІЯоЖЈВЮЙлШЫЪ§ЪЧЖрЩйЃПУХЦБМлИёгІЪЧЖрЩйЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com