
【题目】如图,EF⊥AC于点F,DB⊥AC于点M,∠1=∠2,∠3=∠C,请问AB与MN平行吗?说明理由.完成下列推理过程:

解:AB∥MN.理由如下:
∵EF⊥AC,DB⊥AC,(已知),
∴∠CFE=∠CMD=90°,( )
∴EF∥DM,( )
∴∠2=∠CDM,( )
∵∠1=∠2,(已知),
∴∠1=∠ ( )
∴MN∥CD,( )
∵∠3=∠C,(已知),
∴AB∥CD,( ),
∴AB∥MN.( )
【答案】垂直的定义;同位角相等,两直线平行;两直线平行,同位角相等;CDM;等量代换;内错角相等,两直线平行;内错角相等,两直线平行;平行于同一直线的两条直线平行.
【解析】
根据平行线的性质定理及判定定理即可解答.
解:AB∥MN.理由如下:
∵EF⊥AC,DB⊥AC,(已知),
∴∠CFE=∠CMD=90°,(垂直的定义)
∴EF∥DM,(同位角相等,两直线平行)
∴∠2=∠CDM,(两直线平行,同位角相等)
∵∠1=∠2,(已知),
∴∠1=∠CDM(等量代换)
∴MN∥CD,(内错角相等,两直线平行)
∵∠3=∠C,(已知),
∴AB∥CD,(内错角相等,两直线平行),
∴AB∥MN.(平行于同一直线的两条直线平行)
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,同位角相等;CDM;等量代换;内错角相等,两直线平行;内错角相等,两直线平行;平行于同一直线的两条直线平行.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是井用手摇抽水机的示意图,支点A的左端是一手柄,右端是一弯钩,点F,A,B始终在同一直线上,支点A距离地面100cm,与手柄端点F之间的距离AF=50cm,与弯钩端点B之间的距离AB=10cm.KT为进水管.

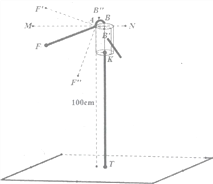
(1)在一次取水过程中,将手柄AF绕支点A旋转到AF′,且与水平线MN的夹角为20°,且此时点B′,K,T在一条线上,求点F′离地面的高度.
(2)当不取水时,将手柄绕支点A逆时针旋转90°至点F′′位置,求端点F′′与进水管KT之间的距离.(忽略进水管的粗细)(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜梁永辉商场今年二月份以每桶40元的单价购进1000桶甲、乙两种食用油,然后以甲种食用油每桶75元、乙桶食用油每桶60元的价格售完,共获利29000元.
(1)求该商场分别购进甲、乙两种食用油多少桶?
(2)为了增加销售量,获得最大利润,根据销售情况和市场分析,在进价不变的情况下该经销商决定调整价格,将甲种食用油的价格在二月份的基础上下调20%,乙种食用油的价格上涨![]() a%,但甲的销售量还是较二月下降了
a%,但甲的销售量还是较二月下降了![]() a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如右图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y3<y2;其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
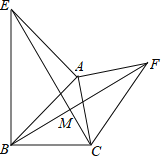
求证:(1)EC=BF;
(2)EC⊥BF;
(3)连接AM,求证:AM平分∠EMF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com