
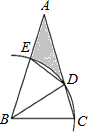
 如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )
如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )| A. | 2$\sqrt{3}$+2-$\frac{5}{6}$π | B. | $\sqrt{3}$+1-$\frac{5}{3}$π | C. | 2$\sqrt{3}$+2-$\frac{1}{2}$π | D. | $\sqrt{3}$+1-$\frac{1}{2}$π |
分析 作DF⊥AB与F,根据等腰三角形的性质求出∠ABD=45°,根据S阴影=S△ABD-S扇形BDE计算即可.
解答  解:作DF⊥AB与F,
解:作DF⊥AB与F,
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
∵BC=BD,
∴∠BDC=∠BCD=75°,
∴∠DBC=30°,
∴∠ABD=∠ABC-∠DBC=45°,
在RT△BDF中,∠FBD=45°,BD=BC=2,
∴BF=DF=BDsin45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
在RT△ADF中,∠A=30°,
∴AD=2DF=2$\sqrt{2}$,AF=$\sqrt{6}$,
∴AB=AF+BF=$\sqrt{6}$+$\sqrt{2}$,
∴S阴影=S△ABD-S扇形BDE
=$\frac{1}{2}$×AB•DF-$\frac{45×π×{2}^{2}}{360}$
=$\sqrt{3}$+1-$\frac{1}{2}$π,
故选:D.
点评 本题考查的是扇形面积的计算,掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键,解答时,要熟记锐角三角函数的定义以及等腰三角形的性质.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知反比例函数的两支图象关于原点对称,利用这一结论解决下列问题:如图,在同一直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D,已知点A(-m,O)、C(m,0).
已知反比例函数的两支图象关于原点对称,利用这一结论解决下列问题:如图,在同一直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D,已知点A(-m,O)、C(m,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
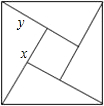 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
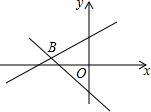 一次函数y=ax+3,与y=bx-1的图象如图所示,其交点B(-3,m),则不等式ax+3>bx-1的解集表示在数轴上正确的是( )
一次函数y=ax+3,与y=bx-1的图象如图所示,其交点B(-3,m),则不等式ax+3>bx-1的解集表示在数轴上正确的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\underbrace{55…5}_{2013个}$ | B. | $\underbrace{55…5}_{2014个}$ | C. | $\underbrace{55…5}_{2015个}$ | D. | $\underbrace{55…5}_{2016个}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com