
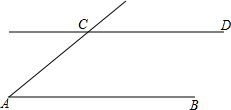
 (2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
(2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于| 1 | 2 |
| 1 |
| 2 |
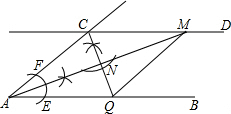 解:(1)把图补充完整(保留痕迹),
解:(1)把图补充完整(保留痕迹),| 1 |
| 2 |
|


科目:初中数学 来源: 题型:
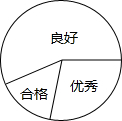 (2013•怀集县二模)九年级(3)班期末考试合格、良好、优秀的比例是1:6:3,小明同学画了一个半径为2cm的圆形的统计图(如图).则表示“良好”的部分的面积是
(2013•怀集县二模)九年级(3)班期末考试合格、良好、优秀的比例是1:6:3,小明同学画了一个半径为2cm的圆形的统计图(如图).则表示“良好”的部分的面积是| 12 |
| 5 |
| 12 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 两点坐标 | 构造 直角三角形 |
一直角边长 | 另一直角 边长 |
斜边长 | ||||||||
| A(1,-2) B(4,2) |
RT△ABC | AC=4-1=3 | BC=2-(-2) | AB=
| ||||||||
| M(-4,2) N(1,-3) |
RT△ MPN MPN |
PN=1-(-4)=5 PN=1-(-4)=5 |
PM=2-(-3)=5 PM=2-(-3)=5 |
MN=
|
| (x-1)2+4 |
| (x-4)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•怀集县二模)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(2013•怀集县二模)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com