在石家庄三年大变样城中村改造时,某村委决定对一段公路进行拓宽改造.已知这项工程由甲工程队单独做需要60天完成;如果由乙工程队先单独做20天,那么剩下的工程还需要两队合做30天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)若乙工程队独做a天后,再由甲、乙两工程队合作______天可完成此项工程;
(3)若甲、乙工程队施工每天需分别付施工费为3万元、1万元,乙工程队至少单独施工多少天后,再由甲乙两队合作完成剩下的工程,才能使施工费不超过110万元?
【答案】
分析:(1)首先设乙工程队单独完成这项工程需x天,由题意得等量关系:乙工程队干20天的工作量+乙工程队干30天的工作量+甲工程队干30天的工作量=1,根据等量关系列出方程解方程即可;
(2)设再由甲、乙两工程队合作y天完成此项工程,由题意得等量关系:乙工程队干a天的工作量+乙工程队干y天的工作量+甲工程队干y天的工作量=1,根据等量关系列出方程解方程即可;
(3)根据(2)可得到方程:乙工程队a天的费用+甲乙两个工程队干

天的费用≤110万元,解不等式即可.
解答:解:(1)设乙工程队单独完成这项工程需x天,由题意得:
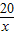
+
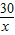
+30×

=1,
解得:x=100,
经检验:x=100是原分式方程的解.
答:乙工程队单独完成这项工程需100天;
(2)设再由甲、乙两工程队合作y天完成此项工程,由题意得:

a+

y+
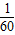
y=1,
解得:y=
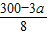
.
故答案为:

;
(3)由(2)得:a×1+
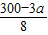
×(3+1)≤110,
解得:a≥80.
答:乙工程队至少单独施工80天后,再由甲乙两队合作完成剩下的工程,才能使施工费不超过110万元.
点评:此题主要考查了分式方程的应用,以及一元一次不等式,一元一次方程的应用,关键是弄懂题意,计算出乙工程队单独完成这项工程需100天,此题用到的公式是:工作效率×工作时间=工作量.

 天的费用≤110万元,解不等式即可.
天的费用≤110万元,解不等式即可.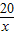 +
+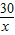 +30×
+30× =1,
=1, a+
a+ y+
y+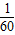 y=1,
y=1,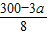 .
. ;
;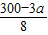 ×(3+1)≤110,
×(3+1)≤110,

 一线名师提优试卷系列答案
一线名师提优试卷系列答案