【答案】
分析:(1)根据二次函数的对称性,已知对称轴的解析式以及B点的坐标,即可求出A的坐标
(2)已知了抛物线过A、B、C三点,而且三点的坐标都已得出,可用待定系数法来求函数的解析式.
(3)本题要先根据抛物线的解析式求出顶点P的坐标,然后求出BP的长,进而分情况进行讨论:
①当∠PQB=∠CAB,即BQ:AB=PB:BC时,根据A、B的坐标可求出AB的长,根据B、C的坐标可求出BC的长,已经求出了PB的长度,那么可根据比例关系式得出BQ的长,即可得出Q的坐标.
②当∠QPB=∠CAB,即BQ:BC=BP:AB,可参照①的方法求出Q的坐标.
③当∠QBP=∠CAB,根据P点和A点的坐标即可得出∠CAO与∠QBP是不相等的,因此∠CAB与∠QBP也不会相等,因此此种情况是不成立的.
综上所述即可得出符合条件的Q的坐标.
解答:
解:(1)∵直线y=-x+3与x轴相交于点B,
∴当y=0时,x=3,
∴点B的坐标为(3,0).
又∵抛物线过x轴上的A,B两点,且对称轴为x=2,
根据抛物线的对称性,
∴点A的坐标为(1,0).
(2)∵y=-x+3过点C,易知C(0,3),
∴c=3.
又∵抛物线y=ax
2+bx+c过点A(1,0),B(3,0),
∴

解,得

∴y=x
2-4x+3.
(3)连接PB,由y=x
2-4x+3=(x-2)
2-1,得P(2,-1),
设抛物线的对称轴交x轴于点M,
∵在Rt△PBM中,PM=MB=1,
∴∠PBM=45°,PB=

.
由点B(3,0),C(0,3)易得OB=OC=3,在等腰直角三角形OBC中,∠ABC=45°,
由勾股定理,得BC=3

.
假设在x轴上存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似.
①当

,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
即

,
∴BQ=3,
又∵BO=3,
∴点Q与点O重合,
∴Q
1的坐标是(0,0).
②当

,∠QBP=∠ABC=45°时,△QBP∽△ABC.
即
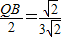
,
∴QB=

.
∵OB=3,
∴OQ=OB-QB=3-

,
∴Q
2的坐标是(

,0).
∵∠PBx=180°-45°=135°,∠BAC<135°,
∴∠PBx≠∠BAC.
∴点Q不可能在B点右侧的x轴上
综上所述,在x轴上存在两点Q
1(0,0),Q
2(

,0),
能使得以点P,B,Q为顶点的三角形与△ABC相似.
点评:本小题主要考查待定系数法、方程、函数及三角形相似等知识,考查综合运用数学知识、分析问题、解决问题的能力,考查数形结合、分类讨论的思想.
此题是一道以函数为背景的综合压轴题,第1、2两个小题较为容易,上手很轻松,第3小题中很容易看出要讨论相似三角形的对应顶角,想提醒大家的是在中考中应该对可能的情况进行逐一讨论,才能尽量防止漏解,如本题中的第3种情况实际上不成立,但最好也讨论一下,有时不成立的情况也会是一个得分点,这样在考场上浪费不了多少时间,却能避免失分的风险.


 解:(1)∵直线y=-x+3与x轴相交于点B,
解:(1)∵直线y=-x+3与x轴相交于点B,

 .
. .
. ,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
,∠PBQ=∠ABC=45°时,△PBQ∽△ABC. ,
, ,∠QBP=∠ABC=45°时,△QBP∽△ABC.
,∠QBP=∠ABC=45°时,△QBP∽△ABC.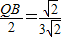 ,
, .
. ,
, ,0).
,0). ,0),
,0),

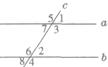 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )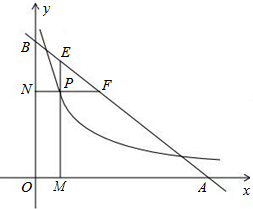 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=