Question

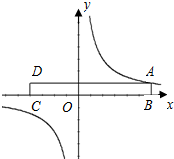
19．如图，将一张长方形的纸片ABCD沿x轴摆放，顶点A（6，1）恰好落在某双曲线上．现在AD边上找一点E，使得将纸片的右半部分沿OE所在直线折叠后，点A恰好还落在此双曲线上，则满足条件的点E的坐标为（1，1）（-1，1）．

Answer 1

分析 由点A（6，1）在双曲线上，求得双曲线函数y=$\frac{6}{x}$，进一步得出AD直线为y=1，设点E为（e，1），则OE直线为y=$\frac{1}{e}$x，点A折叠后为点A'（a，$\frac{6}{a}$）在双曲线函数上．A和A'关于直线OE即y=$\frac{1}{e}$x对称．A和A'的中点（$\frac{a}{2}$+3，$\frac{3}{a}$+$\frac{1}{2}$）在OE直线上，$\frac{1}{e}$（$\frac{a}{2}$+3）=$\frac{3}{a}$+$\frac{1}{2}$…①；AA'与直线OE垂直，所以：AA'的斜率和OE的斜率乘积为-1：$\frac{1-\frac{6}{a}}{6-a}$=-e…②；联立①②解得：a=-1，e=-1或者：a=1，e=1所以：点E为（-1，1）或者（1，1）；由此得出答案即可．

解答 解：点A（6，1）在双曲线y=$\frac{k}{x}$上，
解得：k=6，
双曲线函数y=$\frac{6}{x}$，
∵AB=1-0=1，
∴AD直线为y=1，
设点E为（e，1），
则OE直线为y=$\frac{1}{e}$x，
∵点A折叠后为点A'（a，$\frac{6}{a}$）在双曲线函数上．
∴A和A'关于直线OE即y=$\frac{1}{e}$x对称，
∴A和A'的中点（$\frac{a}{2}$+3，$\frac{3}{a}$+$\frac{1}{2}$）在OE直线上，
∴$\frac{1}{e}$（$\frac{a}{2}$+3）=$\frac{3}{a}$+$\frac{1}{2}$…①；
∵AA'与直线OE垂直，
∴AA'的斜率和OE的斜率乘积为-1，
∴$\frac{1-\frac{6}{a}}{6-a}$=-e…②；
联立①②解得：
a=-1，e=-1或者a=1，e=1；
∴点E为（-1，1）或（1，1）．
故答案为：（1，1）（-1，1）．

点评 此题考查折叠的性质，待定系数法求函数解析式，一次函数相交的问题，利用一次函数图象上点的坐标特征建立方程组是解决问题的关键．