
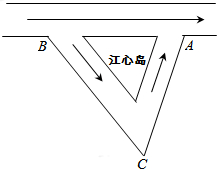
 如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时到达C点,总共行驶了208千米,已知游艇在静水中的速度是38千米/小时.
如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时到达C点,总共行驶了208千米,已知游艇在静水中的速度是38千米/小时.分析 (1)设水流速度为x千米/小时,则顺流航行速度为(38+x)千米/小时,逆流航行的速度为(38-x)千米/小时,根据路程=速度×时间即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据路程=速度×时间分别算出AB、BC段的路程,再根据时间=路程÷速度即可得出返回所需时间.
解答 解:(1)设水流速度为x千米/小时,则顺流航行速度为(38+x)千米/小时,逆流航行的速度为(38-x)千米/小时,
根据题意得:3(38-x)+2.5(38+x)=208,
解得:x=2.
答:水流的速度为2千米/小时.
(2)由(1)可知,顺流航行速度为40千米/小时,逆流航行的速度为36千米/小时.
AB段的路程为3×36=108(千米),
BC段的路程为2.5×40=100(千米),
故原路返回时间为:$\frac{100}{36}$+$\frac{108}{40}$≈2.8+2.7=5.5(小时).
答:游艇用同样的速度原路返回大约需要5.5小时.
点评 本题考查了一元一次方程的应用,解题的关键是:(1)根据路程=速度×时间列出关于x的一元一次方程;(2)根据路程=速度×时间分别算出AB、BC段的路程.


科目:初中数学 来源: 题型:解答题
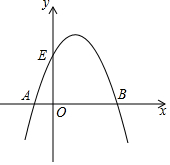 已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.
已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
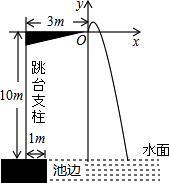 如图,2016年里约奥运会上,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为$10\frac{2}{3}$米.
如图,2016年里约奥运会上,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为$10\frac{2}{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | |
| 甲种货车(辆) | 2 | 5 |
| 乙种货车(辆) | 3 | 6 |
| 累计运货(吨) | 13 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
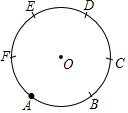 尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )
尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )| A. | ② | B. | ①② | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$×5$\sqrt{3}$=15$\sqrt{3}$ | B. | 3$\sqrt{2}$$+2\sqrt{3}$=5$\sqrt{6}$ | C. | $\sqrt{8}$$-\sqrt{6}$=$\sqrt{2}$ | D. | $\sqrt{60}$$÷\sqrt{5}$=2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com