
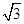 ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE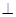 BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )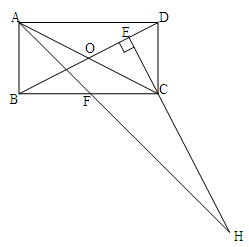
| A.1个 | B.2个 | C.3个 | D.4个 |
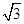 ,AB=1根据特殊角的锐角三角函数值可求出∠ADB=30°,即得∠ABO=60°,从而可证得△ABO是等边三角形,即得AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,再依次分析各小题即可作出判断.
,AB=1根据特殊角的锐角三角函数值可求出∠ADB=30°,即得∠ABO=60°,从而可证得△ABO是等边三角形,即得AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,再依次分析各小题即可作出判断.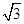 ,AB=1,
,AB=1, ,
, DO=
DO= BD,
BD,

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com