
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,他们的运动时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由
(2)判断此时线段PC和线段PQ的关系,并说明理由。
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变,设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由。
【答案】(1)△ACP≌△BPQ,理由见解析;
(2)PC=PQ且PC⊥PQ,理由见解析;
(3)存在;![]() 或
或![]() .
.
【解析】
(1)利用SAS证得△ACP≌△BPQ;
(2)由(1)得出PC=PQ,∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(3)分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
解:(1)如图(1),△ACP≌△BPQ,理由如下:
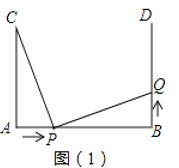
当t=1时,AP=BQ=1,
∴BP=AC=3,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
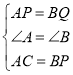 ,
,
∴△ACP≌△BPQ(SAS).
(2)PC=PQ且PC⊥PQ,理由如下:
由(1)可知△ACP≌△BPQ
∴PC=PQ,∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
∴PC⊥PQ.
(3)如图(2),分两种情况讨论:
当AC=BP,AP=BQ时,△ACP≌△BPQ,则
![]() ,
,
解得![]() ,
,
当AC=BQ,AP=BP时,△ACP≌△BQP,则,
![]()
解得![]()
综上所述,存在![]() 或
或![]() 使得△ACP与△BPQ全等.
使得△ACP与△BPQ全等.


科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() ,
,![]() .这样小明就找到了一种把类似
.这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法解决下列问题:
(1)当![]() 、
、![]() 、
、![]() 、
、![]() 均为正整数时,若
均为正整数时,若![]() ,用含
,用含![]() 、
、![]() 的式子分别表示
的式子分别表示![]() 、
、![]() ,得
,得![]() _________,
_________,![]() _________.
_________.
(2)利用所探索的结论,填空:![]() (_____+_____
(_____+_____![]() )2;
)2;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均为正整数,求
均为正整数,求![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为等边三角形,
为等边三角形,![]() 点坐标为
点坐标为![]() ,点
,点![]() 为
为![]() 轴上位于
轴上位于![]() 点上方的一个动点,以
点上方的一个动点,以![]() 为边向
为边向![]() 的右侧作等边
的右侧作等边![]() ,连接
,连接![]() ,并延长
,并延长![]() 交
交![]() 轴于点
轴于点![]() .
.

(1)求证:![]() ;
;
(2)当点![]() 在运动时,
在运动时,![]() 是否平分
是否平分![]() ?请说明理由;
?请说明理由;
(3)当点![]() 在运动时,在
在运动时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,请求出点
为等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AC=BC,∠ACB=90°,CE与AB相交于点D,且BE⊥CE,AF⊥CE,垂足分别为点E、F.
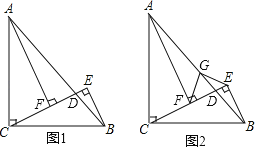
(1)若AF=5,BE=2,求EF的长.
(2)如图2,取AB中点G,连接FC、EC,请判断△GEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com