
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为D.
的顶点为D.
(1)求点D的坐标(用含m的代数式表示);
(2)若该抛物线经过点A(1,m),求m的值;
(3)在(2)的条件下,抛物线与x轴是否有交点,若有,求出交点坐标,若没有,说明理由.
【答案】(1)顶点坐标为D(m,-m+2);
(2)m=3或m=1;
(3)与x轴交点为(2,0),(4,0).
【解析】试题分析:(1)将二次函数解析式化为顶点式,写出顶点坐标即可;(2)将点A的坐标代入二次函数解析式求出m即可;(3)令y=0得到一元二次方程,对此方程的进行有无实数根的判断即可得出抛物线与x轴有无交点.
试题解析:
解:(1)y=x2-2mx+m2-m+2=(x-m)2-m+2,所以顶点坐标为D(m,-m+2).
(2)将A(1,m)代入二次函数解析式得:m= 1-2m+m2-m+2,m2-4m+3=0,
解得:m=3或m=1.
(3)当m=1时,y= x2-2x +2,令y=0,得x2-2x +2=0,
Δ=b2-4ac=(-2)2-4×1×2=-4<0,所以方程无解,所以与抛物线与x轴没有交点;
当m=3时,y= x2-6x +8,令y=0,得x2-6x +8=0,解得x=2或4,
所以抛物线与x轴交点为(2,0),(4,0).


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )

A. 13B. 14C. 15D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() a2b)2(﹣9ab)÷(-
a2b)2(﹣9ab)÷(-![]() a3b2);
a3b2);
(2)(x+2y)(x﹣2y)﹣(x+y)(x﹣y);
(3)[(2a+b)2﹣(a﹣b)(3a﹣b)﹣a]÷(﹣![]() a),其中a=﹣1,b=
a),其中a=﹣1,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图①,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接AE,则AE与BD有怎样的数量关系?说明理由.
(2)类比猜想:如图②,若点D是等边△ABC的边BA延长线上一动点,连接CD,以CD为边在CD上方作等边△CDE,连接AE,请直接写出AE与BD满足的数量关系,不必说明理由;
(3)深入探究:如图③,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边分别在CD上方、下方作等边△CDE和等边△CDF,连接AE,BF则AE,BF与AB有怎样的数量关系?说明理由.
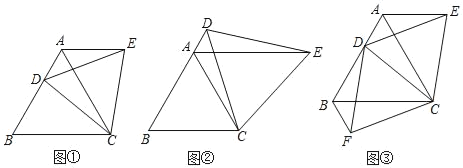
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.
(1)若商场平均每天要盈利1600元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB平分∠CBD,∠DBC=60°,∠C=∠D.
(1)若AC⊥BC,求∠BAE的度数;
(2)请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图,过点D作DG∥BC交CE于点F,当∠EFG=2∠DAE时,求∠BAD的度数.
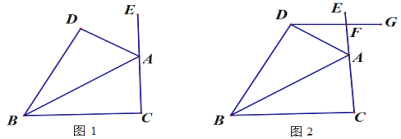
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com