
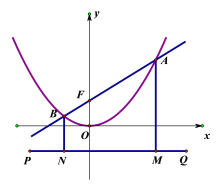
【题目】已知直线l:y=kx+4与抛物线y=![]() x2交于点A(x1,y1),B(x2,y2).
x2交于点A(x1,y1),B(x2,y2).
(1)求:![]() ;
;![]() 的值.
的值.
(2)过点(0,-4)作直线PQ∥x轴,且过点A、B分别作AM⊥PQ于点M,BN⊥PQ于点N,设直线l:y=kx+4交y轴于点F.求证:AF=AM=4+y1.
(3)证明:![]() +
+![]() 为定值,并求出该值.
为定值,并求出该值.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)联立y=kx+4与y=![]() x2,根据一元二次方程根与系数的关系即可求出
x2,根据一元二次方程根与系数的关系即可求出![]() 、
、![]() 的值;
的值;
(2)作FC⊥AM于点C,可求F(0,4).设A(x1 ![]() x1),根据勾股定理及图形与坐标的关系可证结论成立;
x1),根据勾股定理及图形与坐标的关系可证结论成立;
(3)求出AF=![]() , BF=
, BF=![]() ,代入
,代入![]() +
+![]() 化简即可.
化简即可.
∵y=kx+4,y=![]() x2,
x2,
∴![]() x2- kx-4=0,
x2- kx-4=0,
∴![]() ,
,
![]() ;
;
∵y1=kx1+4,y2=kx2+4,
∴![]() ;
;
(2)作FC⊥AM于点C,
∵当x=0时,
y=0+4=4,
∴F(0,4).
设A(x1 ![]() x12),
x12),
∴AF=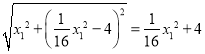 .
.
∵AM=![]() ,
,
∴AF=AM.
∵y1=![]() x12,
x12,
∴AF=AM=4+y1;
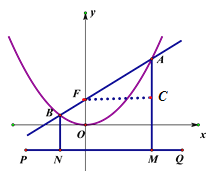
(3)由(2)知,AF=![]() ,同理可求BF=
,同理可求BF=![]() .
.
∴![]() +
+![]()
=
=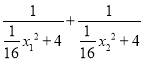
= ![]() .
.
∵ y2+(-8-16k2)y+16=0,
∴![]() ,
,![]() ,
,
∴![]() +
+![]() =
=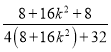
= ![]() .
.


科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下:
(1)自变量x的取值范围是 ,x与y的几组对应值列表如下:
x | … | -3 | - | -2 | -1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | -1 | 0 | -1 | 0 |
| 3 | … |
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分并观察函数图象,写出该函数的两条性质.
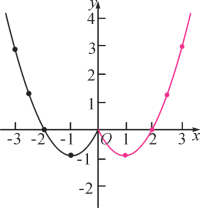
(3)进一步探究函数图象发现:关于x的方程2x2-4|x|=a有4个实数根,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
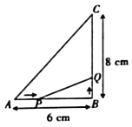
(1)点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果点
的速度移动.如果点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 同时出发,经过几秒,
同时出发,经过几秒,![]() 的面积等于
的面积等于![]() ?
?
(2)点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果点
的速度移动.如果点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 同时出发,线段
同时出发,线段![]() 能否将
能否将![]() 分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点![]() 沿线段
沿线段![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度向点
的速度向点![]() 移动,点
移动,点![]() 沿射线
沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,
的速度移动,![]() ,
,![]() 同时出发,问几秒后,
同时出发,问几秒后,![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC为等腰三角形,AB=AC=a,P点是底边BC上的一个动点,PD∥AC,PE∥AB.
⑴用a表示四边形ADPE的周长为 ;
⑵点P运动到什么位置时,四边形ADPE是菱形,请说明理由;
⑶如果△ABC不是等腰三角形(图2),其他条件不变,点P运动到什么位置时,四边形ADPE是菱形(不必说明理由).
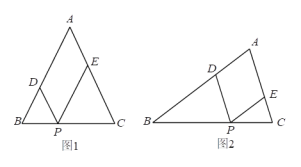
查看答案和解析>>
科目:初中数学 来源: 题型:
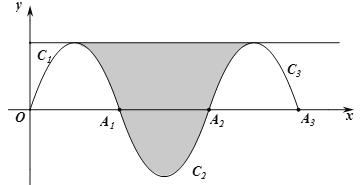
【题目】如图,一段抛物线:![]() ,记为
,记为![]() ,它与
,它与![]() 轴交于两点
轴交于两点![]() ,
,![]() :将
:将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() :将
:将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() .过抛物线
.过抛物线![]() ,
,![]() 顶点的直线与
顶点的直线与![]() ,
,![]() ,
,![]() 围成的如图中的阴影部分,那么该面积为_________.
围成的如图中的阴影部分,那么该面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
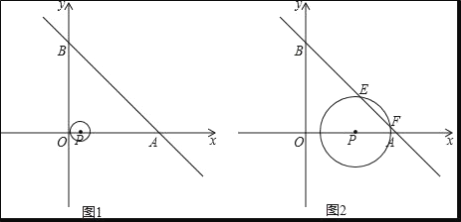
【题目】如图1,一次函数y=﹣x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的⊙P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时⊙P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为 ,点B的坐标为 ,∠OAB= °;
(2)在运动过程中,点P的坐标为 ,⊙P的半径为 (用含t的代数式表示);
(3)当⊙P与直线AB相交于点E、F时
①如图2,求t=![]() 时,弦EF的长;
时,弦EF的长;
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
查看答案和解析>>
科目:初中数学 来源: 题型:
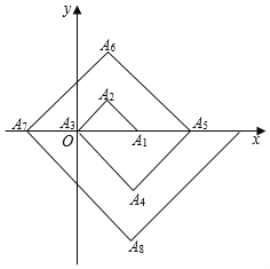
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
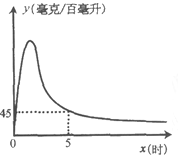
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
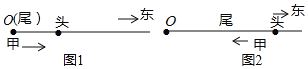
【题目】长为![]() 的春游队伍,以
的春游队伍,以![]() 的速度向东行进,如图1和图2,当队伍排尾行进到位置
的速度向东行进,如图1和图2,当队伍排尾行进到位置![]() 时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为![]() ,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置![]() 开始行进的时间为
开始行进的时间为![]() ,排头与
,排头与![]() 的距离为
的距离为![]()
(1)当![]() 时,解答:
时,解答:
①求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围);
的取值范围);
②当甲赶到排头位置时,求![]() 的值;在甲从排头返回到排尾过程中,设甲与位置
的值;在甲从排头返回到排尾过程中,设甲与位置![]() 的距离为
的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
(2)设甲这次往返队伍的总时间为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围),并写出队伍在此过程中行进的路程.
的取值范围),并写出队伍在此过程中行进的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com